MATH1051 Lecture Notes - Lecture 15: Indeterminate Form, Partial Fraction Decomposition

Lecture #15 – 7.5/7.8 - Improper Integrals
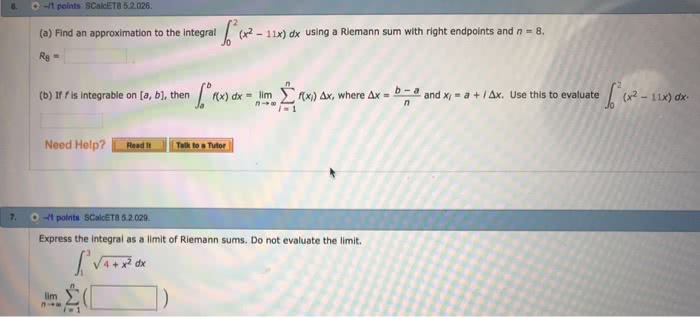
Reviewing the definition of an integral
●(x)dx (x)Δx
∫
b
a
f= lim
n→∞ ∑
n
k=1
fk
●What does this mean?
○The integral of the function on the interval from to ,(x)f a b
○Is the limit of the sum of multiplied by the change of x(x)fk
●Whenever we have some number in that is NOT in the domain of , thea,b][ (x)f
integral is said to be improper
Example #1
●dx
∫
∞
1
1
x2
○We know this is improper because of the boundary of ∞
○How do we solve this?
○Think about replacing with a different variable∞
○dxlim
T→∞ ∫
T
1
1
x2
■We can take the limit as T goes to ∞
■And then replace with T in the integral to make it possible to solve for∞
■After taking the integral, we would then take the limit
○dxlim
T→∞ ∫
T
1
x−2
○(from 1 to T)lim
T→∞ −1
x−1
○( )lim
T→∞ − 1
T− − 1
T
■Then we can take the limit after simplifying
○1 lim
T→∞ − 1
T

■The limit as 1 approaches is just 1∞
■The limit as approaches is 0
1
T∞
○ 0 11 − =
○So the answer is 1
■Because the limit is a definitive number, and not an answer such as ,+ ∞
or , it is said to convergent− ∞
Example #2
●dx
∫
∞
1x
1
○dxlim
T→∞ ∫
T
1x
1
○n from 1 to T)lim
T→∞ l x
| | (
○n lnlim
T→∞ l T
| | − 1
| |
○n0lim
T→∞ l T
| | −
■The limit as T approaches on is ∞nl T
| | + ∞
■Because the answer is NOT a definitive number, the limit is said to be
divergent
Example #3
●e dx
∫
0
−∞
xx
○e dxlim
T→ −∞ ∫
0
T
xx
■From here, we notice that we have a not so easy integral to evaluate
■Use integration by parts
○ x,therefore du (1)dxu = =
○v e dx,therefore v ed = x = x
Document Summary
Reviewing the definition of an integral b a f (x)dx. = lim n n k=1 f (x ) x k. Is the limit of the sum of f (x ) k. Whenever we have some number in f (x) on the interval from a to b multiplied by the change of x a, b] that is not in the domain of f (x) , the integral is said to be improper. We know this is improper because of the boundary of . Think about replacing with a different variable. We can take the limit as t goes to . After taking the integral, we would then take the limit. T with t in the integral to make it possible to solve for. Then we can take the limit after simplifying. Because the limit is a definitive number, and not an answer such as or. T n l t| n l t| dx from 1 to t ) ln.