HomeClass Notes1,200,000CA670,000

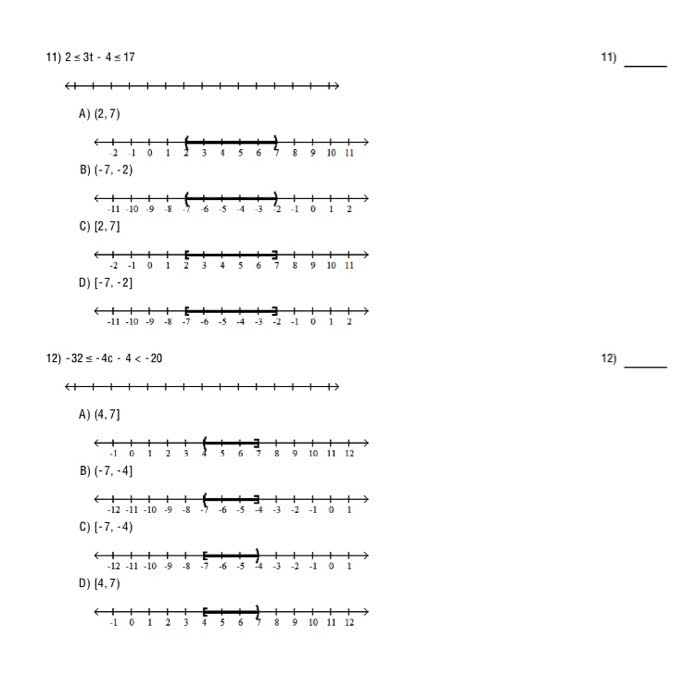
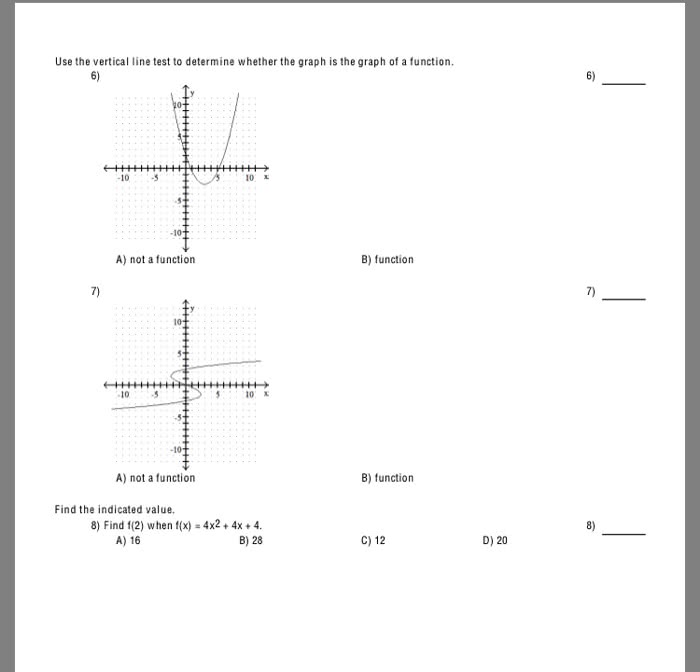
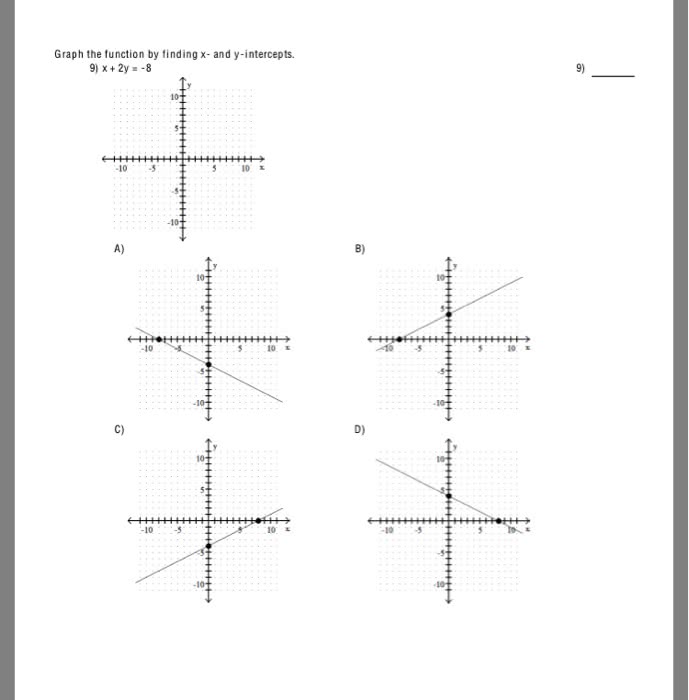
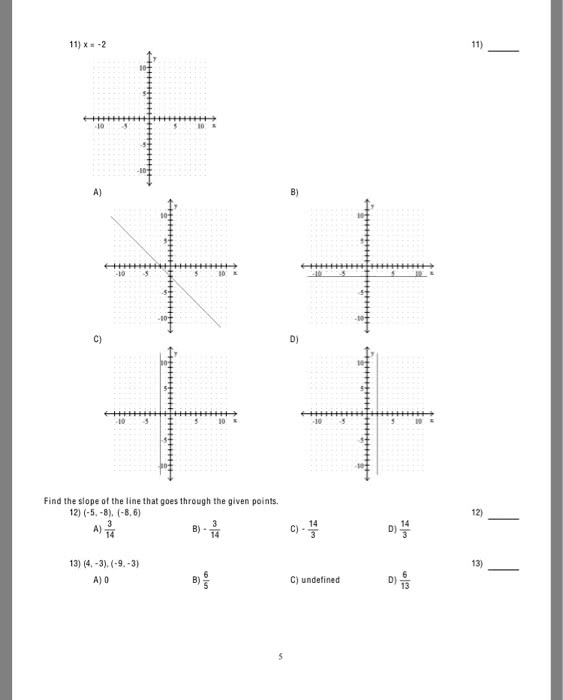
MACM 101 Lecture 17: Lecture 17 Part 2_ Cardinality

32 views3 pages

browncricket987

21 Dec 2018

School

Simon Fraser University

Department

Math & Comp Sci

Course

Professor

For unlimited access to Class Notes, a Class+ subscription is required.

Document Summary

Sets that are not countable are called uncountable countable sets: finite sets any subset of n. In other words we can make a list of all integers. 0, 1, -1, 2, -2, 3, -3, 4, -4, 5, -5, . The cardinality of the set of all natural numbers is denoted by 0. The set of positive rational numbers is countable. Every rational number can be represented as a fraction p/q. We do not insist that p and q do not have a common divisor. This gives an injection from q+ to n. the converse injection is f(x) = x + 1. If a is an infinite set, then | a | 0. Every real number can be represented as an infinite decimal fraction, like. Suppose we have constructed a list of all real numbers. Let bi = 4 if aii 4.

Related textbook solutions

Calculus

ISBN: 9781319050733

Single Variable Calculus: Early Transcendentals

4th Edition, 2018

ISBN: 9781337687805

CALCULUS:EARLY TRANSCENDENTALS

ISBN: 9781319050740

Related Documents

MACM 101 Lecture 17: Lecture 17 Part 1_ Cardinality

browncricket987

MACM 101 Lecture 12: Lecture 12 Part 1_ Sets

browncricket987

MACM 101 Study Guide - Final Guide: Omen, Universal Instantiation, If And Only If

burgundyoyster925

Related Questions

Consider the integers with the normal operation of addition.

On which of these subsets of the integers is addition "closed" ? (select all that are correct)

a)	The natural numbers: {1, 2, 3, ... }

b)	The multiples of 3: {..., -6, -3, 0, 3, 6, ...}

c)	The odd integers: {..., -3, -1, 1, 3, 5, ...}

d)	The nonnegative integers less than 5: {0, 1, 2, 3, 4}

22

ey table is seen below xeecions tor Chapter 1 12, Fori, b â¬ Î.el * b-aa (0 (D 14 ForVEQ r the operation defined in Example 1 on the wr John Sue Henry. P iDFor 15ine if is ass ociative by determining if the final six engu defined ang property (ii)of Theorem 1 . So no element i if the operntion debined in Example 1 of Emle if each element has an inverse Section 1.3 Groups iw comutatityn ild Chapter 3 where the Funda the exercises that follow etermining why they are not Write out the Cayley table for the gru(o)nud lensify thee element the 10 elements of the group Z 18 its operation uses ts in the first coordinnte and +2 in the secotu Ldessity the Zn and write out the Cayley table. Reeall th of each element does Theorem 1.14 tell us aont the entries in the Cayley table ol s xrewp that is set with exactly one element. A {n), will always form group since there 19. What nly one way to define an operation on the set. Be sure to shhow that the properi combination of the usual notice what set the rule is be of a group all hold. 21. We can create even create groupe with games! Consider four cups placed in a ssare patter table. If we have a penny in one of the cups there are four ways we can move it to t cup: Horizontally, Vertically, Diagonally, or Stay nehere it is. We will p, S. To define nn operation, consider two movements in a row, v.e.,m ove the penny as r tells us to, then after that move the penny as y instruets. the set of integers the set of real numbers n the set of positive integers. e set of positive integers. n the set of positive integers. on the set of integers e set of negative integers. we ple, HV D since if we first move it horizontally and then vertically nltogether e moved it diagonally. Create the Cayley table for this group, identify the identity and the inverse of cach element 22. Prove that the set A 0 under matrix multiplication. Is it abelian? 23. Verify that 3(R) is a group using the addition of funetions as defined in Example 13 e set of nonzero rational n he set of nonzero real num n on the set R (-1 Section 1.4 Basic Algebra in Groups 24. Prove the Cancellation Law (Theorem 1.20). Do not use any theorems that occur after it in the text ssociative, commutative, has roof or counterexample fo 25. Assume G is a group and a e G. Consider a fixed integer k and use PMI (Theorem 0.3) to prove that for all nEN, a aYou will need to consider cases here since k can be positive, negative, or o 26. Prove Theorem 1.23 (ii) for the case of n > 0 and m