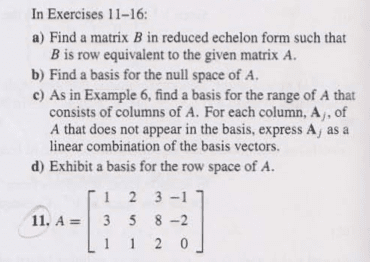MATH125 Lecture Notes - Lecture 23: Row And Column Spaces, Identity Matrix

• School: University of Alberta
• Department: Mathematics
• Course: MATH125
• Professor: Nikita

Document Summary

There are three prominent vector subspaces related to a matrix a, namely row(a), nul(a) and col(a). The next example shows that the standard procedure for writing the solution set of ax = 0 in a parametric vector form actually allows one to produce a basis for nul a. Find a basis for the null space of the matrix. The null space of a is the set of all solutions of the equation. We also know that the linear system whose coe cient matrix is the reduced echelon form of a has the same set of solutions. Applying elementary row operations to the augmented matrix [a | 0 ] we nd that a reduced echelon form of a is. 0 hence the general solution is x1 = 2x2 + x4 3x5 x3 = 2x4 + 2x5 x2 x4 x5 is free is free is free x1 x2 x3 x4 x5 x2. It follows the solution x in a vector form is.