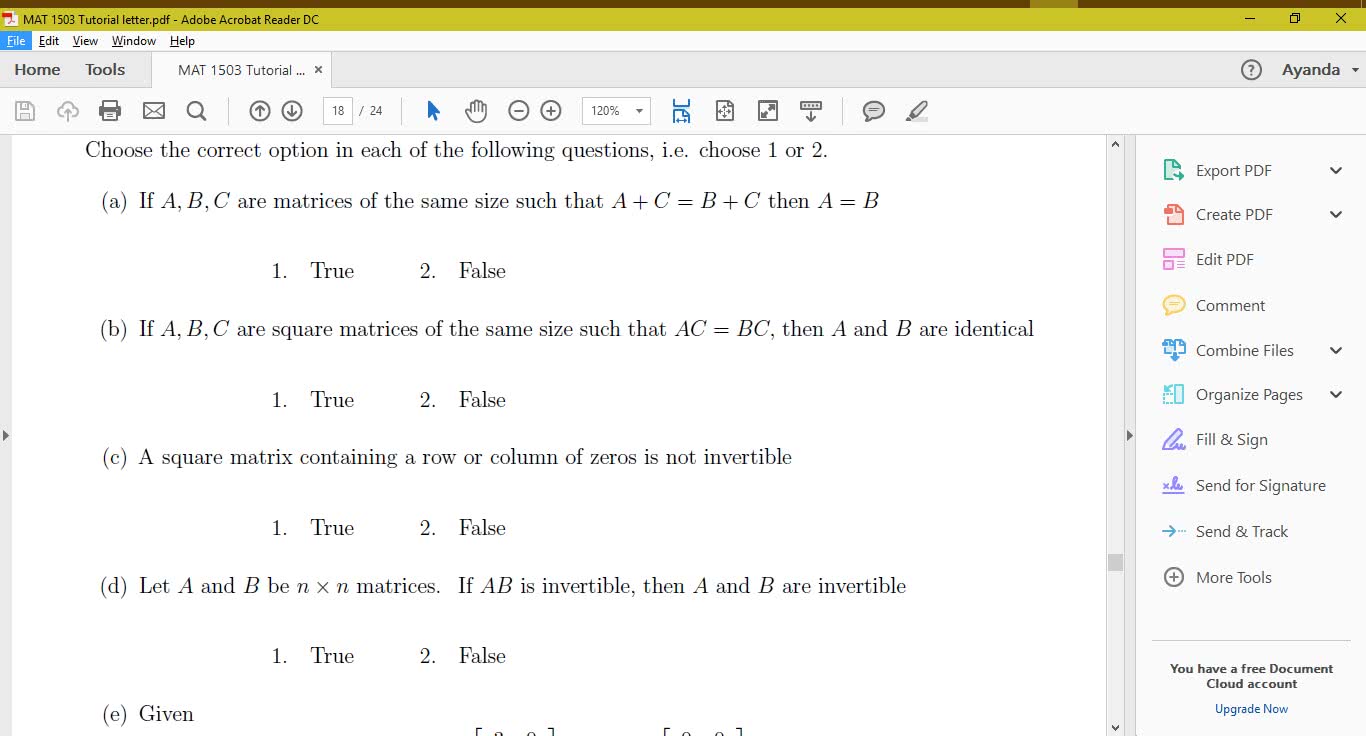
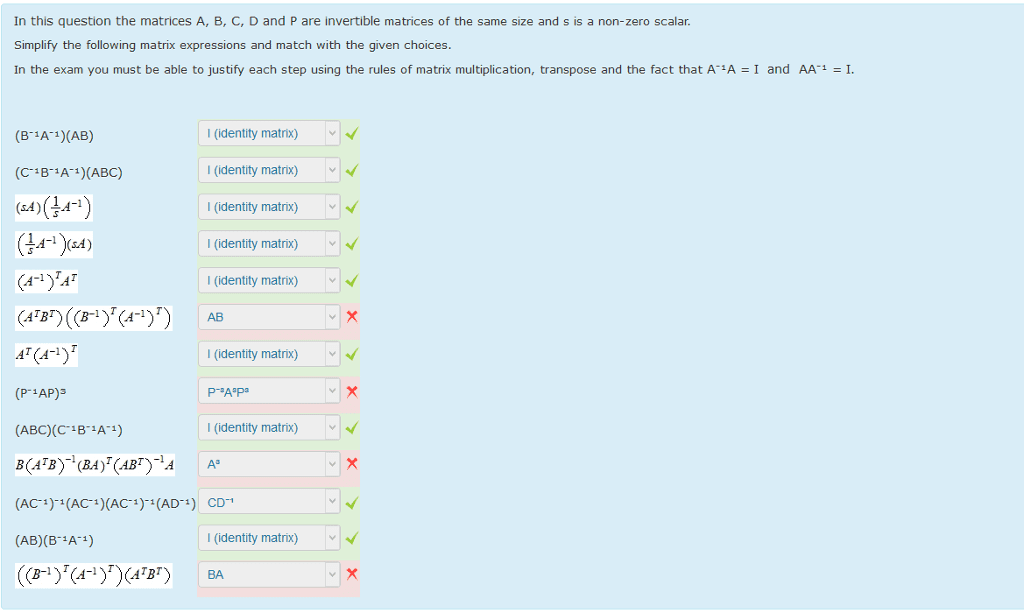
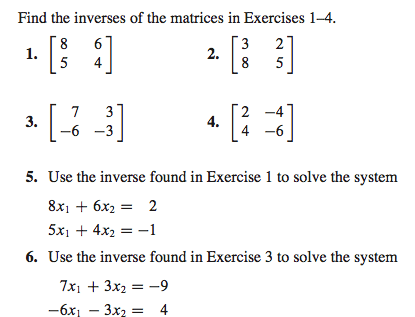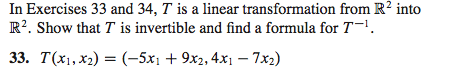MATH125 Lecture Notes - Lecture 7: Elementary Matrix, Row And Column Vectors, Identity Matrix

• School: University of Alberta
• Department: Mathematics
• Course: MATH125
• Professor: Vladimir Chernousov

Document Summary

For scalars, the inverse is denoted by 1/n. For example: the inverse of 3 is . Definition: a square matrix a of size nxn is called invertible if there exists another matrix b of size nxn such that ab=in=ba, therefore the matrices a and b must commute. Notation: if b exists then it is denoted a-1 and is called the inverse of a. Remark: the inverse for a, if it exists, is unique. Theorem: assume you are given a linear system in matrix form ax=b where a is a square matrix. Then if a is invertible, the system has a unique solution given by the formula: x=a-1b. Proof: indeed, let us check that the column vector a-1b is a solution, that is, it =x. A(a-1b)=(aa-1)b=inb this symbol indicates it is the end of the proof. *note: you do not need to memorize proofs for exams, you just need to know what the outcome of a proof is.