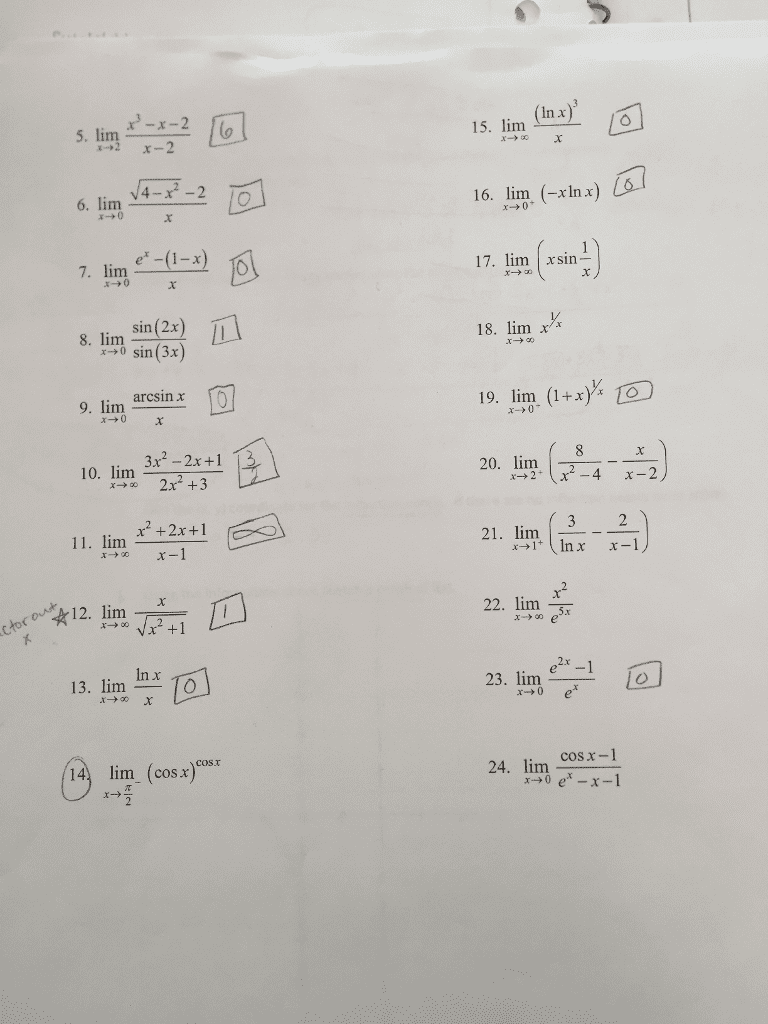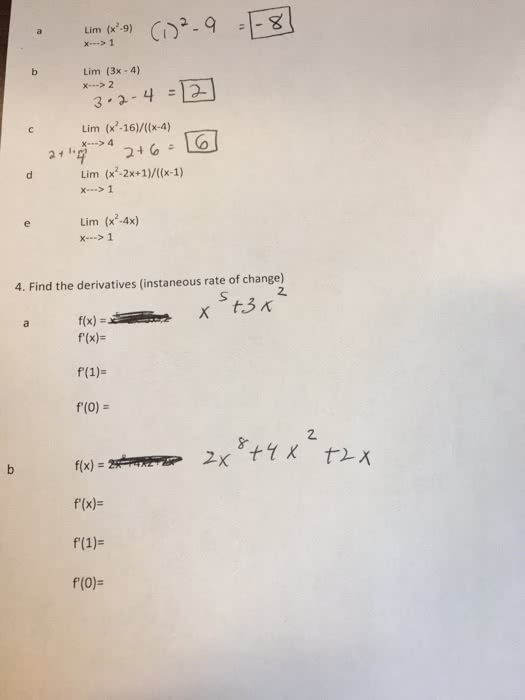MATH116 Lecture 5: M116F15_P3

• School: University of Waterloo
• Department: Mathematics
• Course: MATH116
• Professor: Fiona Dunbar

Document Summary

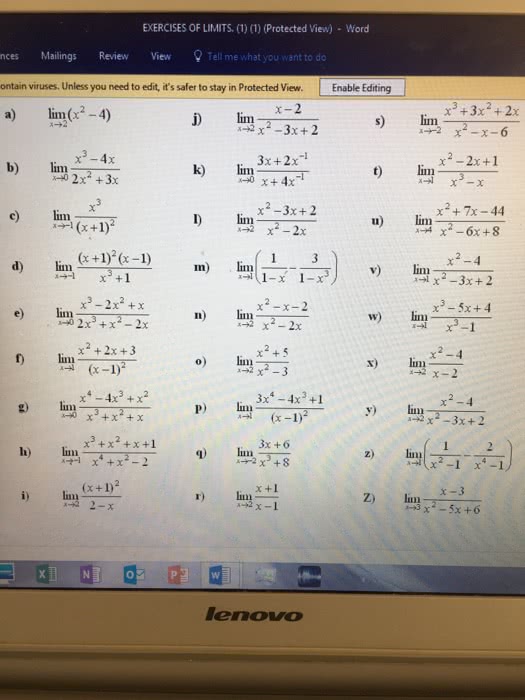
Practice problems 3: (a) solve log5 (x + 4) + log5 (x) = 1 for x. (b) solve 4x + 2x+1 = 18 for x. (c) solve ln. < 0. (cid:18)3x 2 (cid:19) x 1: evaluate the following limits if they exist. |x2 + x 2| x2 + x 4 4 (cid:18) (cid:19) 1 x2 1 x2 1 arctan ax 2b x2 bx + a x < 1. 1 x < 1 x 1 f (x) : show that sin 1(tanh x) = tan 1(sinh x). Hint: let = sin 1(tanh x), . = tan 1(sinh x), that = , since the tan function is one-to-one on ( /2, /2). If you can prove that tan = tan , then that will prove.