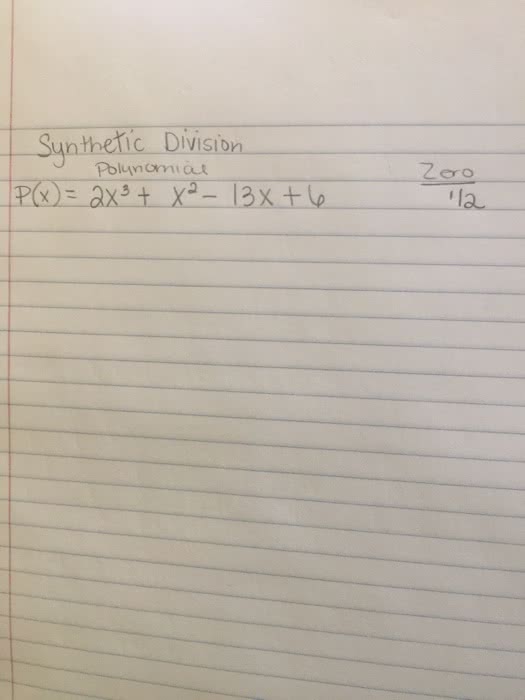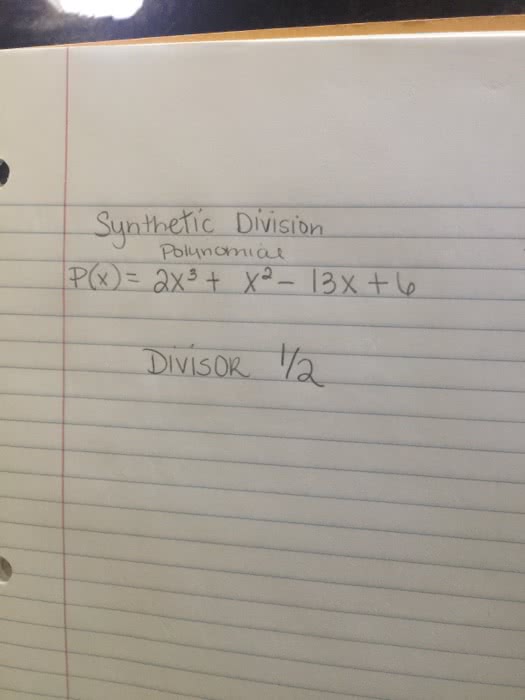MATH116 Lecture Notes - Lecture 14: Opata Language
9 Dec 2015
School
Department
Course
Professor
Document Summary
9x6 x x3 + 1: find the limit lim x . Notice the highest power of x appearing is e ectively x3, since the x6 is under a square x6, to make sure we have all the signs root. However, we divide the top and bottom by correct. Since x , this means x < 0, which means positive number, but x3 would then be negative. To compensate for the negativity of x3, we multiply by 1 to make the whole thing positive: 9x6 x x3 + 1 lim x . = lim x (cid:16) 1 (cid:16) 1 x6 x6 (cid:17) (cid:17) = lim x . 1 0 (cid:16) 1 (cid:0) 1 x3 x6 (cid:17) (cid:1) = lim x (cid:113) 9x6 x (cid:0) x3+1 x3 (cid:1) x6. = lim x : make a careful sketch of the graph of y = f (x) = ln(x), and below it sketch the graph of y = f(cid:48)(x).
