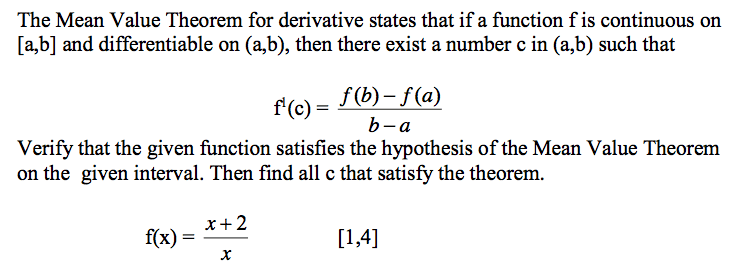MATH 100 Lecture Notes - Lecture 4: Mean Value Theorem

Math 100
Lesson 3.2 – Rolle’s Theorem
• Introduction:
The Extreme Value Theorem states that a continuous function on a closed interval [a,b]
must have both a minimum and a maximum on the interval. Both of those, however,
can occur at the endpoints. Rolle’s Theorem gives conditions that guarantee the
eistee of a etrea i the iterior of a losed iteral.
• Theore .: Rolle’s Theore
Let f be continuous on the closed interval [a,b] and differentiable on the open interval
(a,b). If f(a) = f(b), the there is at least oe uer i a, suh that f’=.
*Note: Fro Rolle’s Theore, ou a see that if a futio f is otiuous o [a,] ad
differentiable on (a,b) and f(a) = f(b), there must be at least one x-value between a and
b at which the graph f has a horizontal tangent. When the differentiability requirement
is dropped fro Rolle’s Theore, if ou ill still hae a ritial uer i a, ut it
may not have a horizontal tangent line.
Example 1: find the two x-intercepts of ad sho that f’= at
some point between the two intercepts.
f(x)=0:
Fro Rolle’s Theore: to fid
Interval includes 3/2.
• Theorem 3.4: The Mean Value Theorem
If f is continuous on the closed interval [a,b] and differentiable on the open interval
a,, the there eists a uer i a, suh that
Example 2: Given
, find all values of c in the open interval (1,4) such that
.
. There eists oe uer i , suh that f’ = .
Since the interval is (1,4) so c = +2.
*Note: there is an alternative form of the Mean Value Theorem and that is:
find more resources at oneclass.com
find more resources at oneclass.com
Document Summary
The extreme value theorem states that a continuous function on a closed interval [a,b] must have both a minimum and a maximum on the interval. Both of those, however, can occur at the endpoints. Rolle"s theorem gives conditions that guarantee the e(cid:454)iste(cid:374)(cid:272)e of a(cid:374) e(cid:454)tre(cid:373)a i(cid:374) the (cid:862)i(cid:374)terior(cid:863) of a (cid:272)losed i(cid:374)ter(cid:448)al: theore(cid:373) (cid:1007). (cid:1007): rolle"s theore(cid:373) some point between the two intercepts. Interval includes 3/2: theorem 3. 4: the mean value theorem. Let f be continuous on the closed interval [a,b] and differentiable on the open interval (a,b). If f(a) = f(b), the(cid:374) there is at least o(cid:374)e (cid:374)u(cid:373)(cid:271)er (cid:862)(cid:272)(cid:863) i(cid:374) (cid:894)a,(cid:271)(cid:895) su(cid:272)h that f"(cid:894)(cid:272)(cid:895)=(cid:1004). When the differentiability requirement is dropped fro(cid:373) rolle"s theore(cid:373), if (cid:455)ou (cid:449)ill still ha(cid:448)e a (cid:272)riti(cid:272)al (cid:374)u(cid:373)(cid:271)er i(cid:374) (cid:894)a,(cid:271)(cid:895) (cid:271)ut it may not have a horizontal tangent line. Example 1: find the two x-intercepts of (cid:1858)(cid:4666)(cid:1876)(cid:4667)=(cid:1876)(cid:2870) (cid:885)(cid:1876)+(cid:884) a(cid:374)d sho(cid:449) that f"(cid:894)(cid:454)(cid:895)=(cid:1004) at f(x)=0: (cid:1876)(cid:2870) (cid:885)(cid:1876)+(cid:884)=(cid:882) (cid:1876)=(cid:883),(cid:1876)=(cid:884). (cid:1858)(cid:4666)(cid:883)(cid:4667)=(cid:1858)(cid:4666)(cid:884)(cid:4667)=(cid:882).