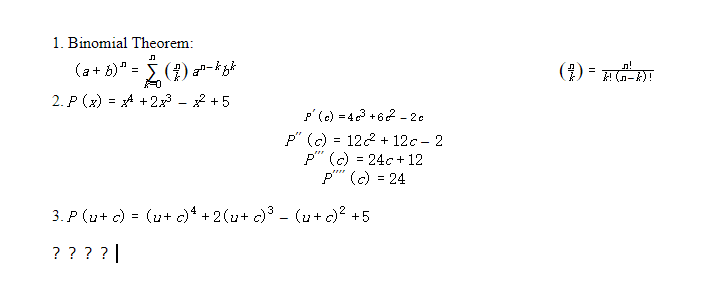MTH 355 Lecture Notes - Lecture 13: Distributive Property

• School: Oregon State University
• Department: Mathematics
• Course: MTH 355
• Professor: T. Schmidt

Document Summary

X in was an arbitrary element of. Prove that if a is an even integer and b is an odd integer then at b is an odd integer a b is even. Given pr#e a is an even integer and b is an odd integer a tb is an odd integer. Suppose a is an even integer and from from b the is an odd integer definition of even. 2k ta the definition of an odd integer n. 2c ktlltl by distributive property of multiplication definition of an odd number since both k and l are integers. { all odd integers } by ktlltl atb is an odd integer. = c x - 2) c x - i ) by distribution of real numbers. C x - 2) ( x - 11=0. X 2-3 1-2 co ( x - 2) c x - d lo exactly one of. I holds with the other factor being negative i #