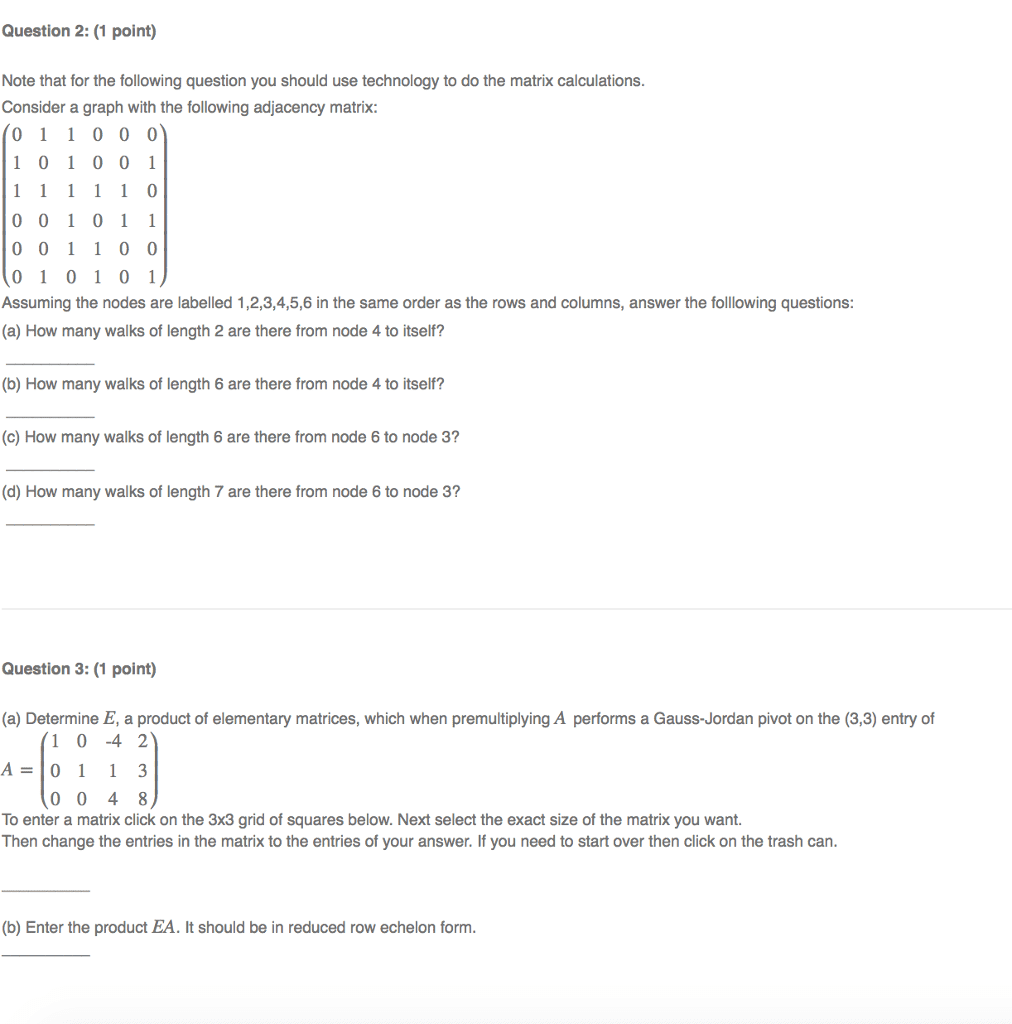
MATH 220 Lecture Notes - Lecture 3: Elementary Matrix, Gaussian Elimination, Row Echelon Form
Document Summary
Math 220 lecture 3 continued 1. 2 row reduction. Row reduction: sequence of operations on a matrix. Formal definition: a matrix, , is row equivalent to a matrix, , if can be transformed to by a series of elementary row operations. *as a consequence of elementary row operations, each matrix is row equivalent to one (unique) reduced row echelon form. The elementary row operations that can be performed on a matrix are the following: multiplying a row through by a nonzero constant, interchanging two rows, adding the multiple of one row to another. Find the reduced row echelon form of the matrix: 1. We want to start by putting the matrix into echelon form first. We do this by checking off the conditions for echelon form. We want the leading terms to have nothing but zeros below them. We can do this by adding the multiple of one row to another to cancel them to zero.