MATH 251 Lecture Notes - System Of Linear Equations, Linear Algebra, Uniqueness Theorem
Document Summary
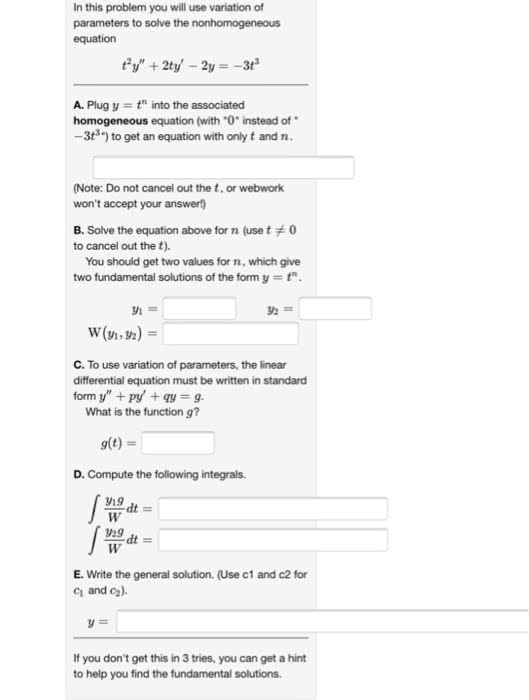
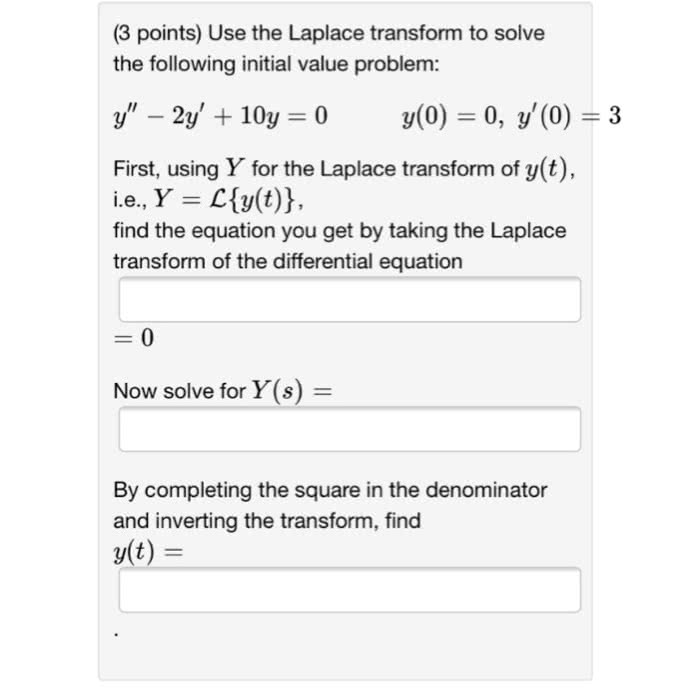
Second order linear equations with constant coefficients; fundamental solutions; wronskian; existence and uniqueness of solutions; the characteristic equation; solutions of homogeneous linear equations; reduction of order. In this chapter we will study ordinary differential equations of the standard form below, known as the second order linear equations: y + p(t) y + q(t) y = g(t). y + p(t) y + q(t) y = 0. Homogeneous equations: if g(t) = 0, then the equation above becomes. Trivial solution: for the homogeneous equation above, note that the function y(t) = 0 always satisfies the given equation, regardless what p(t) and q(t) are. This constant zero solution is called the trivial solution of such an equation. Second order linear homogeneous differential equations with constant coefficients. For the most part, we will only learn how to solve second order linear equation with constant coefficients (that is, when p(t) and q(t) are constants).