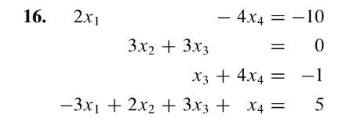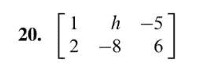MATH 240 Lecture Notes - Lecture 3: Matrix Multiplication, Scalar Multiplication
11 Jul 2017
School
Department
Course
Professor
Document Summary
So in the last section, we used matrices to solve systems of linear equations without ever telling you what a matrix was. A matrix is an array of numbers enclosed by two brackets. [(cid:885) (cid:883) (cid:891)] (cid:887) (cid:888)(cid:889) (cid:882) (cid:886)(cid:887) (cid:884) columns. The size of a matrix is denoted by (cid:1853) (cid:1854) where (cid:1853) is the number of rows and (cid:1854) is the number of. So in the examples of matrices above, we see the first matrix is a (cid:884) (cid:883), the second is a (cid:883) (cid:883), and the third is a (cid:885) (cid:885). A matrix with the same number of rows and columns is called a square matrix because just like a square, the length and width are the same. Note that all matrix operations require you to have two matrices of the same size. For example, you can"t add a (cid:885) (cid:883) matrix to a (cid:885) (cid:885) matrix. Perform the following operations on the following matrices:
