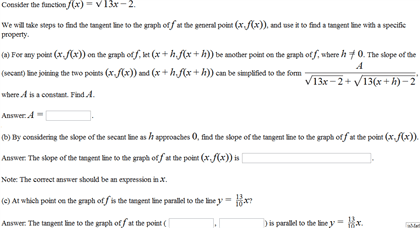MATH 1271 Lecture 3: 3.10- Linear Approximations & Differentials
Document Summary
3. 10- linear approximations & differentials tangent line to the graph of f at a y=f"(a)(x-a)+f"(a) this came from the point-slope formula for a line with the slope m=f"(a) point (x , y )=(a,f(a)) define the function. L(x)=f"(a)(x-a)+f(a) x appears in only one spot, and is the variable a is a constant, depending on where we took our tangent line. So, we can use l(x) to approximate values of f(x) Use the linear approximation of f(x)= (x) at x=4 to estimate (3), (3. 5), (3. 9) find f"(x) derivative slope of tangent line points for formula. Since y=l(x) lies above the graph of y= (x) our estimates are over- estimates. The closer we are to the point of tangency, the better our approximation is! Choose an a value so that f(a), f"(a) are easy to evaluate by hand and our given x is close to a find l(x) use f(x) is approximate l(x) to estimate!