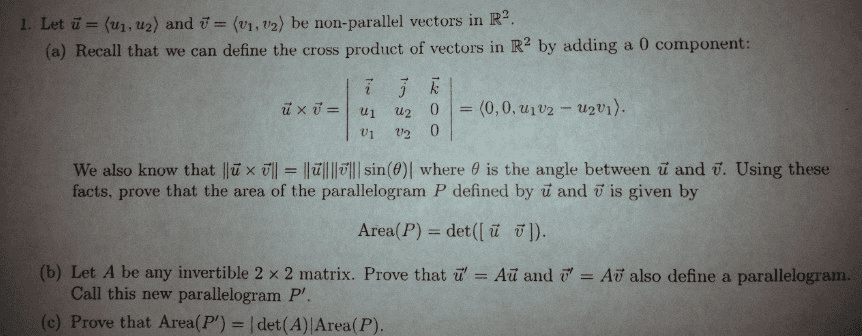MA 35100 Lecture Notes - Lecture 32: Parallelogram, Parallelepiped, Talking Lifestyle 1278
Document Summary
=take [rectorsinr" e. g. ), 3], and make a parallelogram. 3) a - c s a - c. Area of i = area of ii area of 8-10 +6) Because area is always (t) and determinants are not, Theorem 4. 12: if a = ca, az] is a 2x2 matrix, then the area of the parallelogram with sides a, az is. This idea extends to any new matrix a: e. g. for a 3x3 matrix. *= [a. , az , ag], a. , az, ay describe a parallelepiped: A z (theorem 4. 12 pt. 2) volume = idet (a) i. It a = ca, az], 2x2 and b is 2x2 (tb: r" -12), then ba: (ba, baz] so b transforms parallelogram w/ sides a. , an into parallelogram with sides ba, and ba, which has area laet (ba) i. I det (ba))= i det (b) ) idet (a) (cid:8869) original parallelogram area. Theorem 4. 1: if p is a parallelogram in and b is 2x2, the parallel piped.