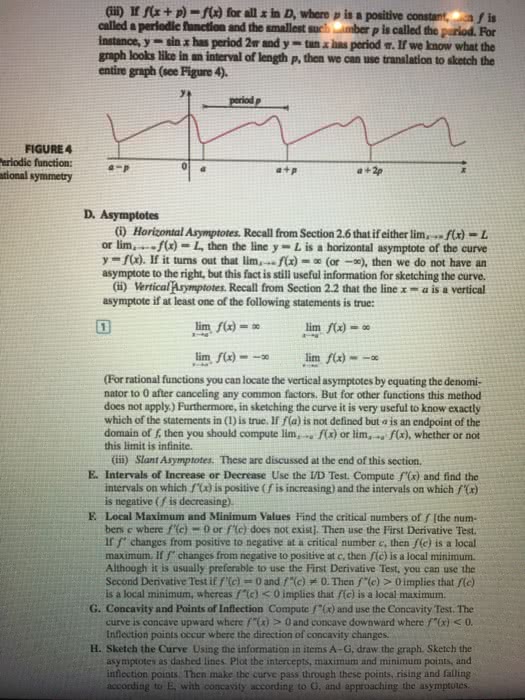
1
answer
0
watching
95
views
13 Nov 2019
Check in each of the following cases , the equation F=0 defines y locally as a continuously differentiable function Ï(x) near a=[x0,y0] and calculate DÏ(x0).
a) F(x,y)=y^2-x^3-2sin(pi(x-y)), x0=1,y0=-1
b) F(x1,x2,y)=e^(x1y) +y^2cos(x1x2)-1, x0=[1 2 ], y0 = 0
Check in each of the following cases , the equation F=0 defines y locally as a continuously differentiable function Ï(x) near a=[x0,y0] and calculate DÏ(x0).
a) F(x,y)=y^2-x^3-2sin(pi(x-y)), x0=1,y0=-1
b) F(x1,x2,y)=e^(x1y) +y^2cos(x1x2)-1, x0=[1 2 ], y0 = 0
Irving HeathcoteLv2
11 Jul 2019
