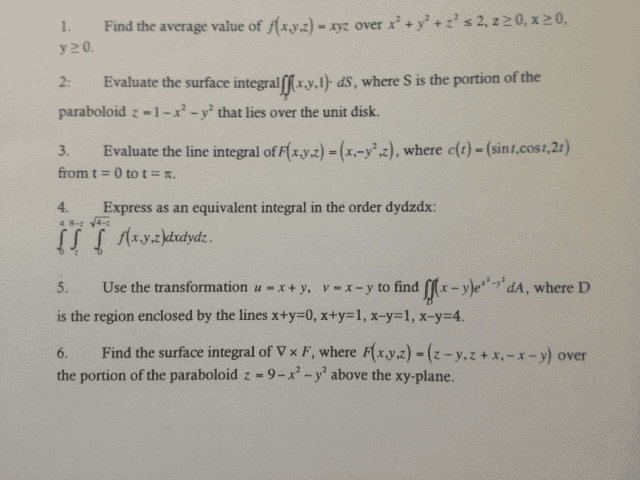MATH 217 Midterm: MATH 217 2005 Winter Test 1
Document Summary
S : cos( x) x2y + exz + yz = 4. (a) find the plane tangent to s at (0, 1, 2). (b) suppose (0. 03, 0. 96, z) lies on s. give an approximate value for z. (c) Show that each critical point of this function gives a local minimum: f (x, y) = 1. Find the centroid (x, y, z) of the solid inside the cylinder x2 + y2 = 4, above the plane z = 0, and below the paraboloid z = 1 + x2 + y2. 1 px2 + y2 dx dy. (a) rewrite i as an iterated integral in polar coordinates. (b) evaluate i. Z sec(at) dt = a 1 ln |sec(at) + tan(at)|, Z csc(at) dt = a 1 ln |csc(t) cot(t)|. Let c be a simple closed curve in the plane 2x + 2y + z = 2, oriented counterclockwise when viewed from high on the z-axis. (a)