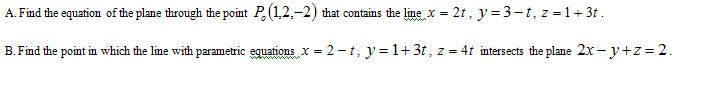MATH 226 Midterm: MATH 226 2005 Winter Test 1
Document Summary
Find all points on the surface 3x2 y2 + 2z2 = 1 where the tangent plane is parallel to both of the vectors (2, 2, 1) and (4, 1, 5). Y and at (x, y) = (1, 0), if z = f (ex+2y, sin(xy), ex y) and f : r3 (6 marks) find. R is a function of class c 1 such that f (e, 0, e) = (1, 1, 2). F (e, 0, e) = (3, 1, 2). (use the chain rule). (b) (4 marks) if f(x, y) =(cid:18) z z2(cid:19) , where z is as in (a), nd df(1, 0). The plane x + 2y + z = 2 intersects the paraboloid z = x2 + y2 in an ellipse. Find the points on this ellipse which are nearest to and farthest from the origin. In each part of this problem, provide a precise de nition of the word or phrase in boldface.