MATH 267 Study Guide - Midterm Guide: Computer Engineering, Inductor, 3I
Document Summary
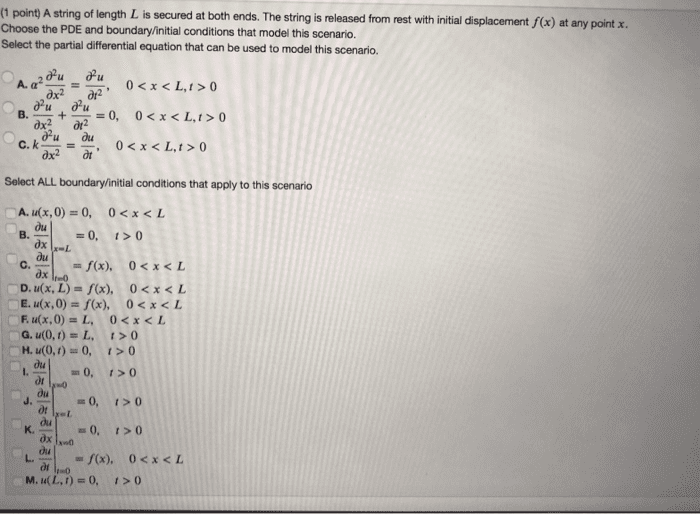
[15] 1. (a) an elastic string of length 4 with xed ends has an initial shape u(x, 0) = f (x), where f (x) =( 0. It is released from rest at time t = 0. Assume that the displacement u(x, t) satis es uxx = utt, Find u(x, t). (b) sketch u(x, 0) and u(x, 1). Let g(x) = x be de ned for 0 x 1. (a) extend g(x) as a periodic function of period 1. Find the fourier series for g(x) in complex form. (b) extend g(x) as an odd function of period 2. Find the fourier series for g(x) in terms of sines and cosines. (c) one end (x = 0) of a copper bar ( 2 = 1) of length 1 is maintained at 0 c while the other is at 10 c. Find the temperature u(x, t) in the bar if u(x, t) satis es ut = uxx.