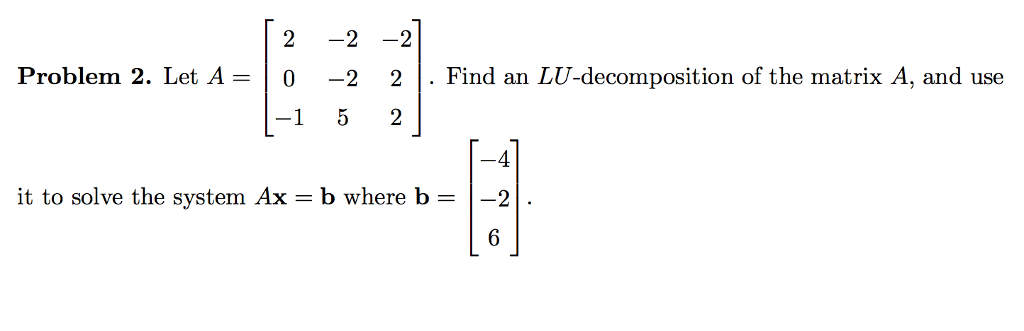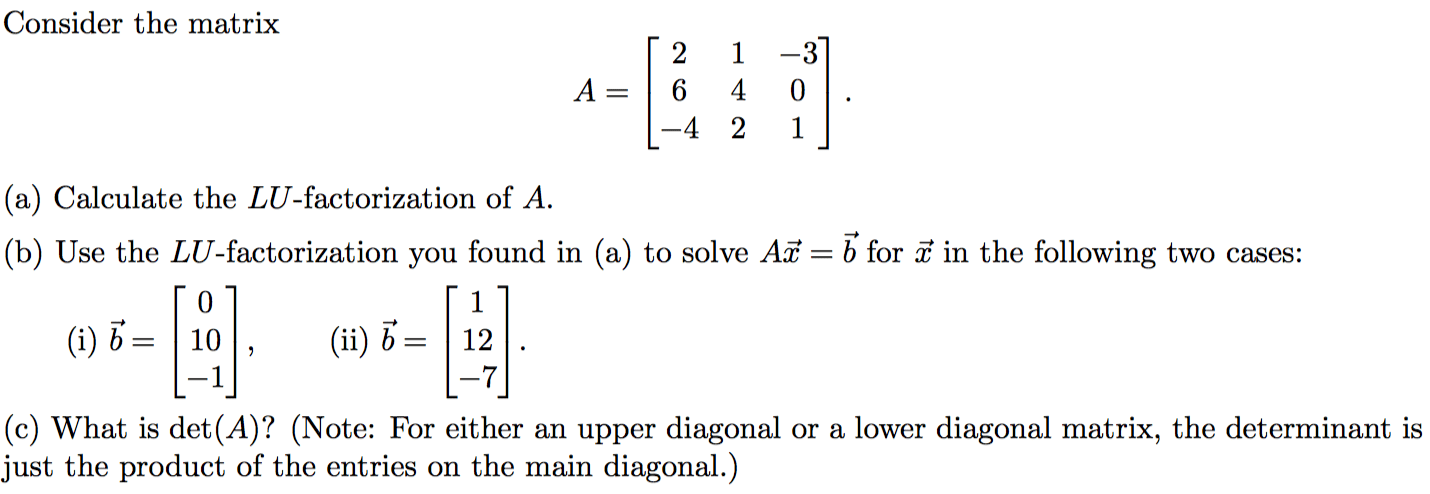MATH 307 Study Guide - Midterm Guide: Lu Decomposition, Matrix Exponential, Invertible Matrix

• School: UBC
• Department: Mathematics
• Course: MATH 307
• Professor: all

Document Summary

[5] compute the lu decomposition of the matrix a = . [5] if x solves the equation ax = . What are the dimensions of the nullspace, the (b) [5] find an orthogonal basis for the space spanned by . Decide whether each of the following statements is true or false. All matrices in this question are square (n n). (a) [3] if a = a 1 then every eigenvalue of a is either 1 or 1. (b) [3] the diagonal entries of an upper triangular matrix are its eigenvalues. (c) [3] eigenvalues of an anti-symmetric matrix (i. e. , at = a) are negative. (d) [3] if s is any invertible matrix, then a and sas 1 have the same determinant. (e) [3] if u and v are orthogonal and a = u v t then a and have the same eigenvalues. (f) [3] if 2 is an eigenvalue of a then 6 is an eigenvalue of a + a2. (g)