MAT-1110 Midterm: MATH 1110 App State Fall2017 Test1 answer key
Document Summary
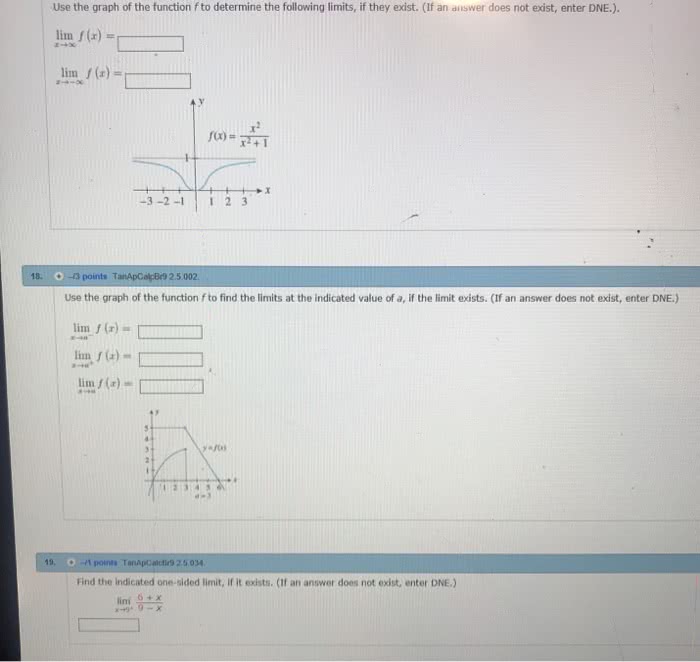
6 x f (0) = lim x 0 f (x) = Dne lim x 3 f (x) = lim x 5+ f (x) = So the limit as x goes to 0 is 0 while the function"s value is f (0) = 1. Thus the sharp corner at x = 2 accounts for f "s lack of di erentiability there. Note: we cannot just plug-in x = 1 since this would result in a division by 0. (b) determine lim x 1. 3x2 3x x2 4x + 3 lim x 1. Since g(x) is not continuous at x = 0, it cannot be di erentiable at x = 0. Just because g(x) is continuous at x = 3 does not necessarily mean it is also di erentiable. For example, g(x) = |x 3| is continuous but not di erentiable at x = 3. (b) suppose that h(x) is di erentiable everywhere and that h(1) = 2 and h(3) = 8.