21127 Study Guide - Final Guide: Enu, Fair Coin, Bijection
16 Dec 2015
School
Department
Course
Professor
Document Summary
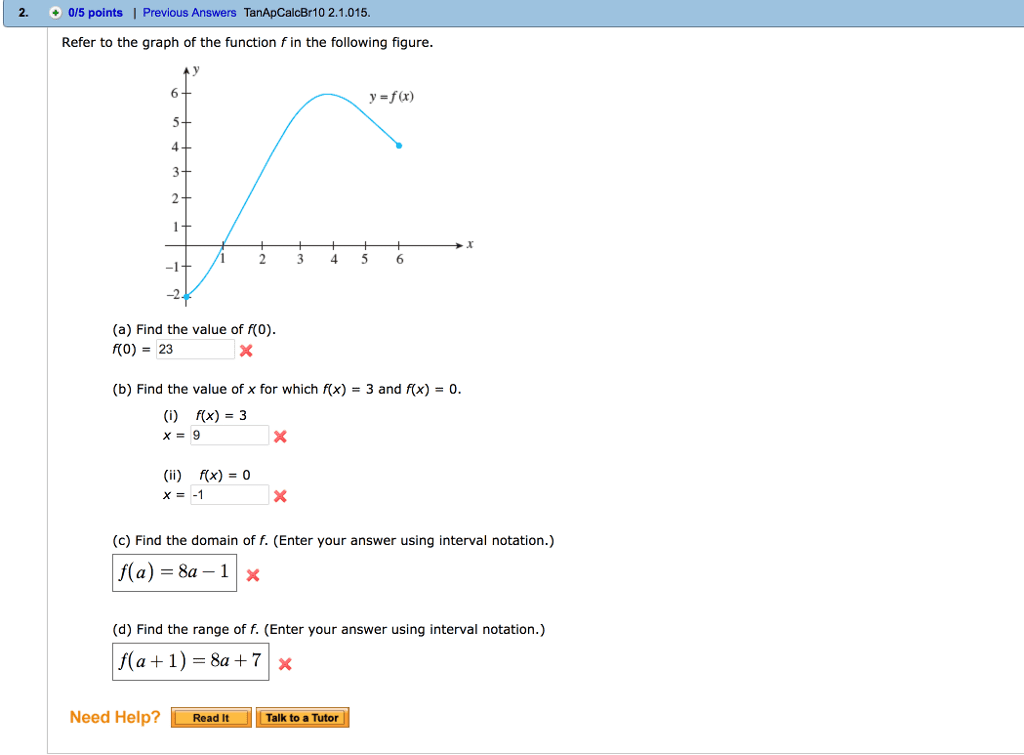
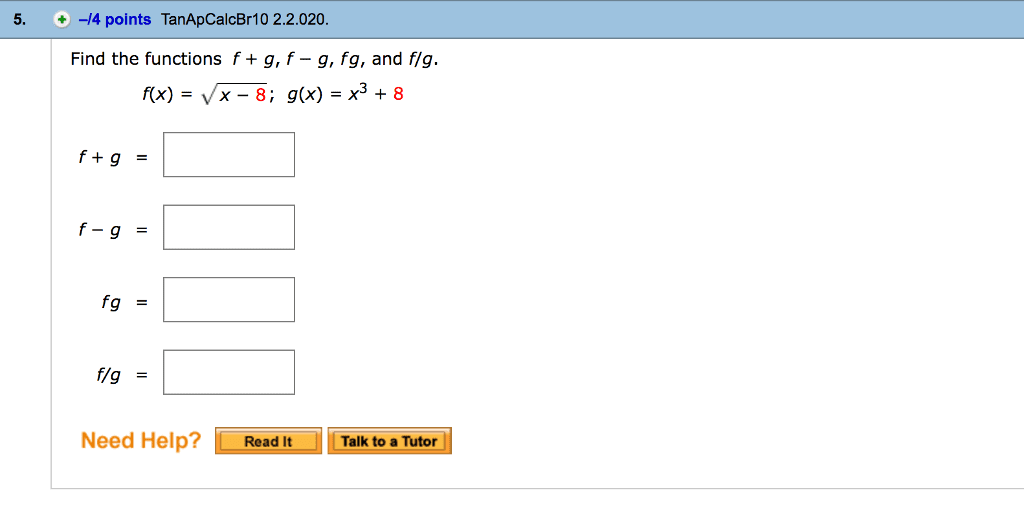
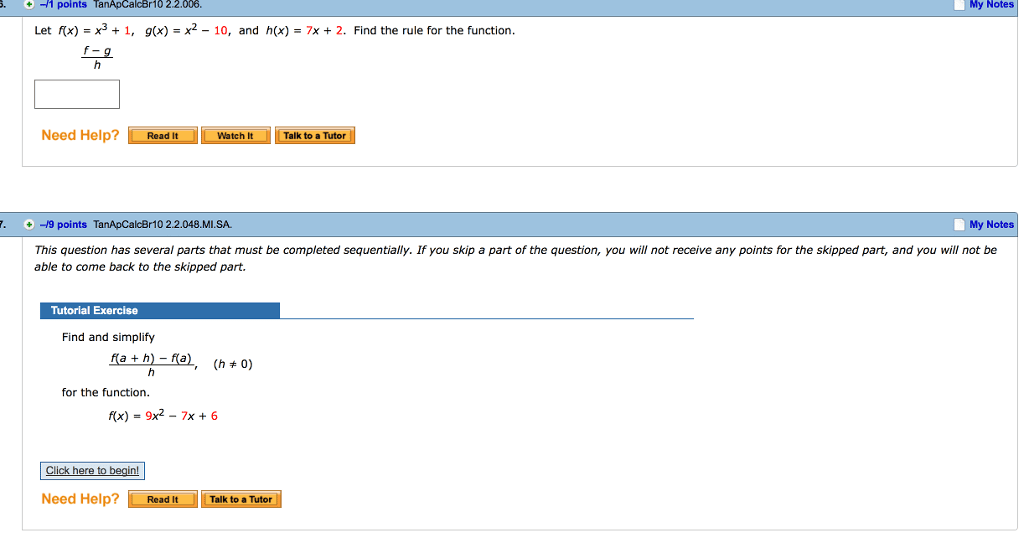
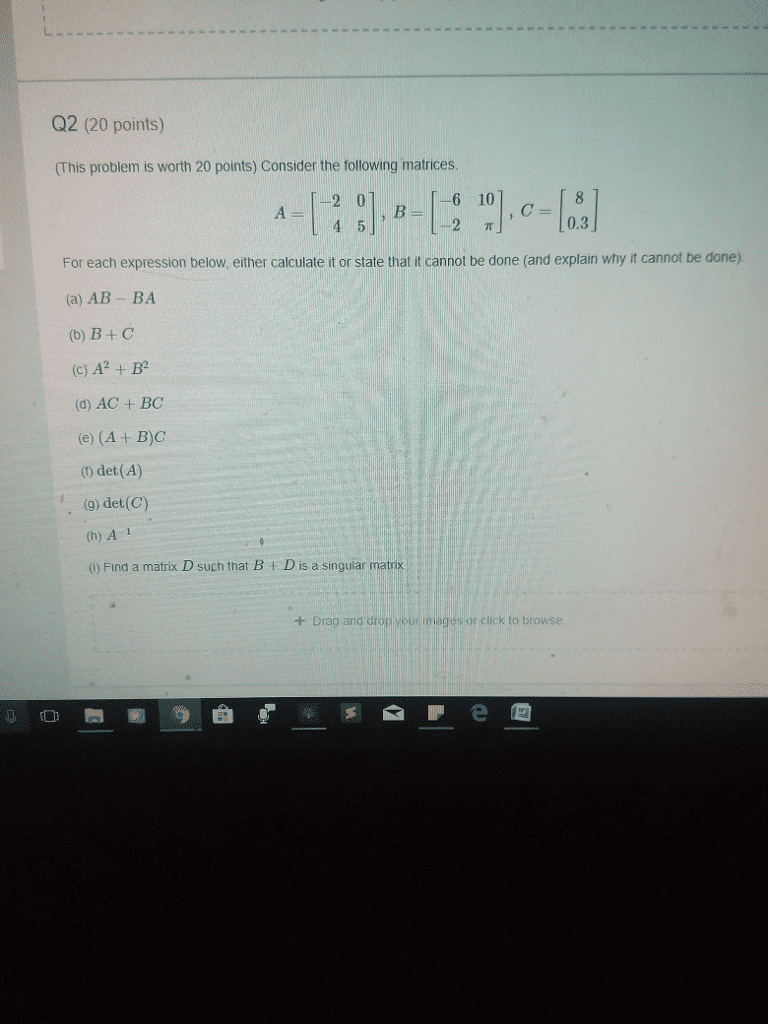
Then we say a | b k z. b = ak. Prove your claim is correct. (5) de ne a sequence recursively as follows: a0 = 1 and an = 4n + an 1 for all n n with n > 0. Prove that an = 2n2 + 2n + 1 for every n n {0}. (6) de ne the sequence of fibonacci numbers by f0 = 0 and f1 = 1 and. That is, f0 = 0, f1 = 1, f2 = 1, f3 = 2, f4 = 3, f5 = 5, and so on. Prove the following claim about the fibonacci numbers by induction: N n {0}. n(cid:88) fk = fn+2 1 (7) prove or disprove the following claim: (a b) c = a (b c) k=0 (8) let s, t be sets of sets. Prove or disprove the following claims: (cid:91) (cid:92) Y t and (9) let a be a nite set.
