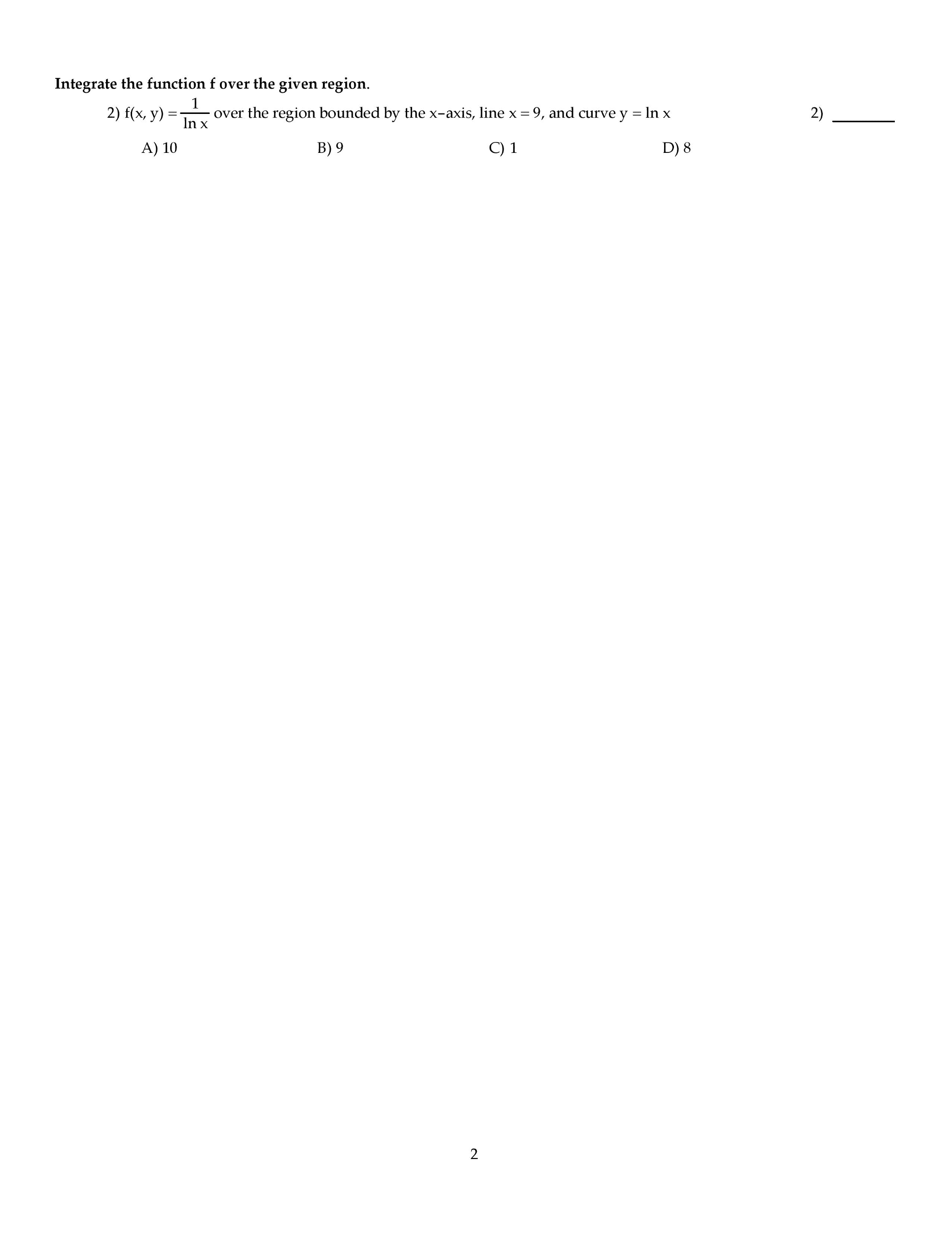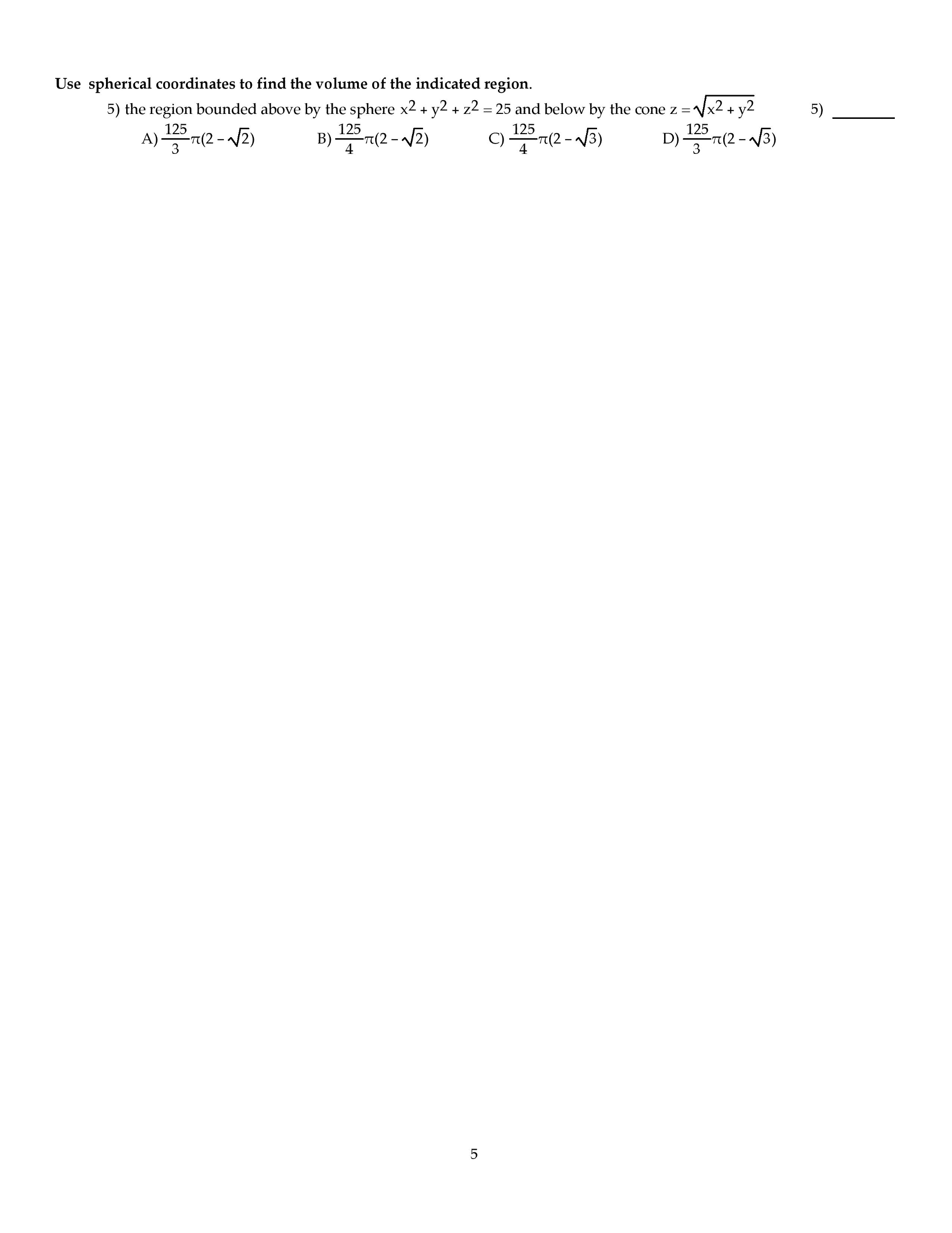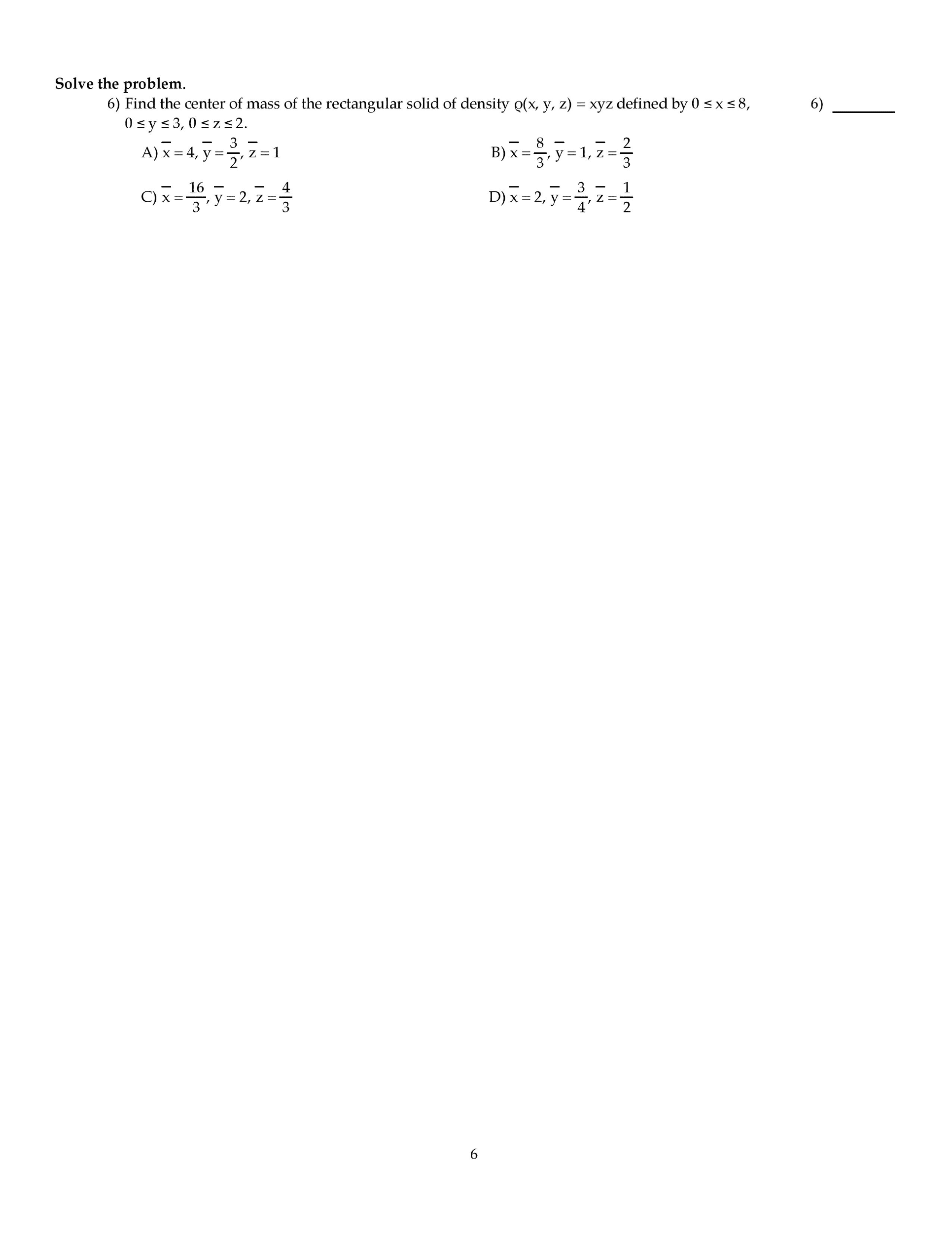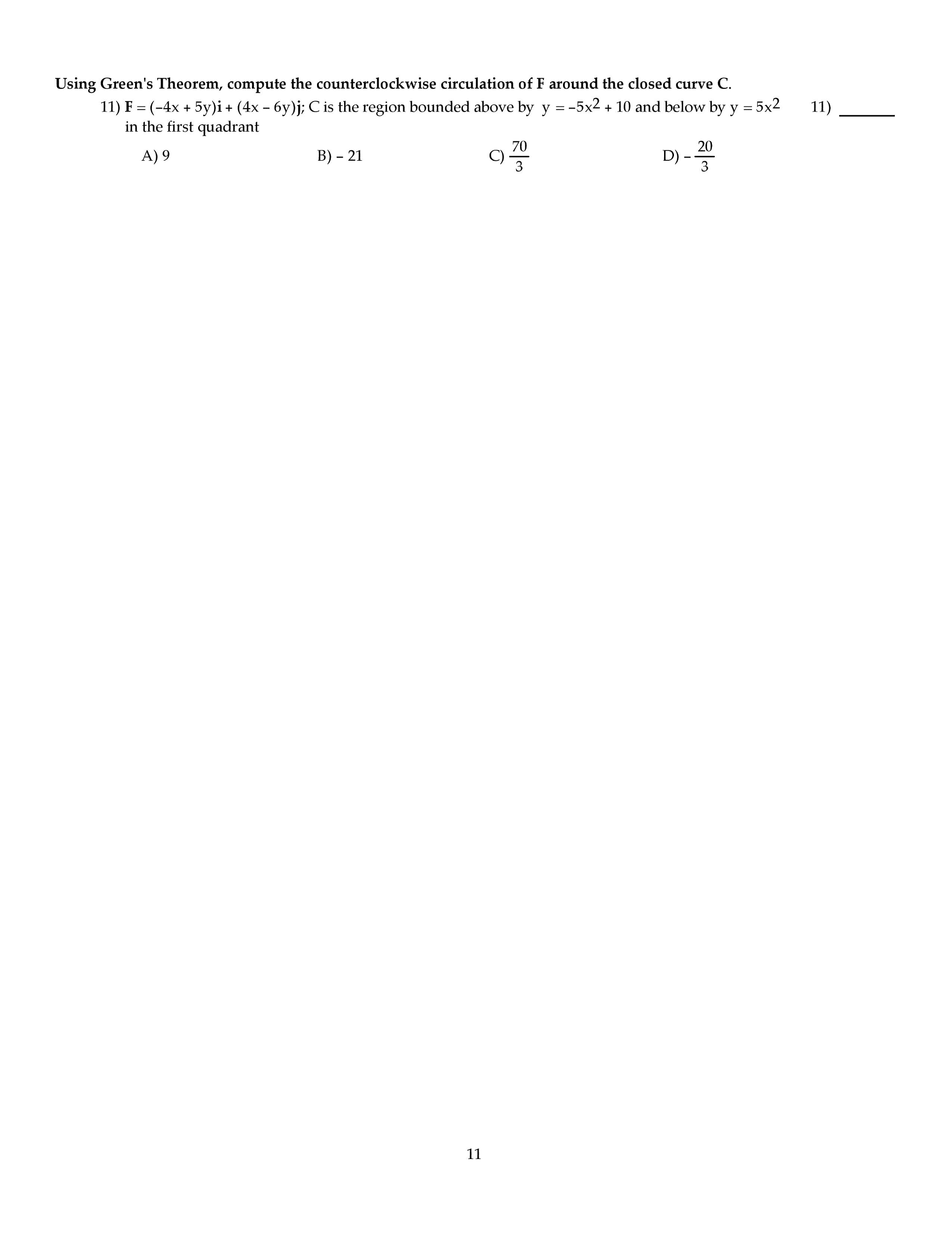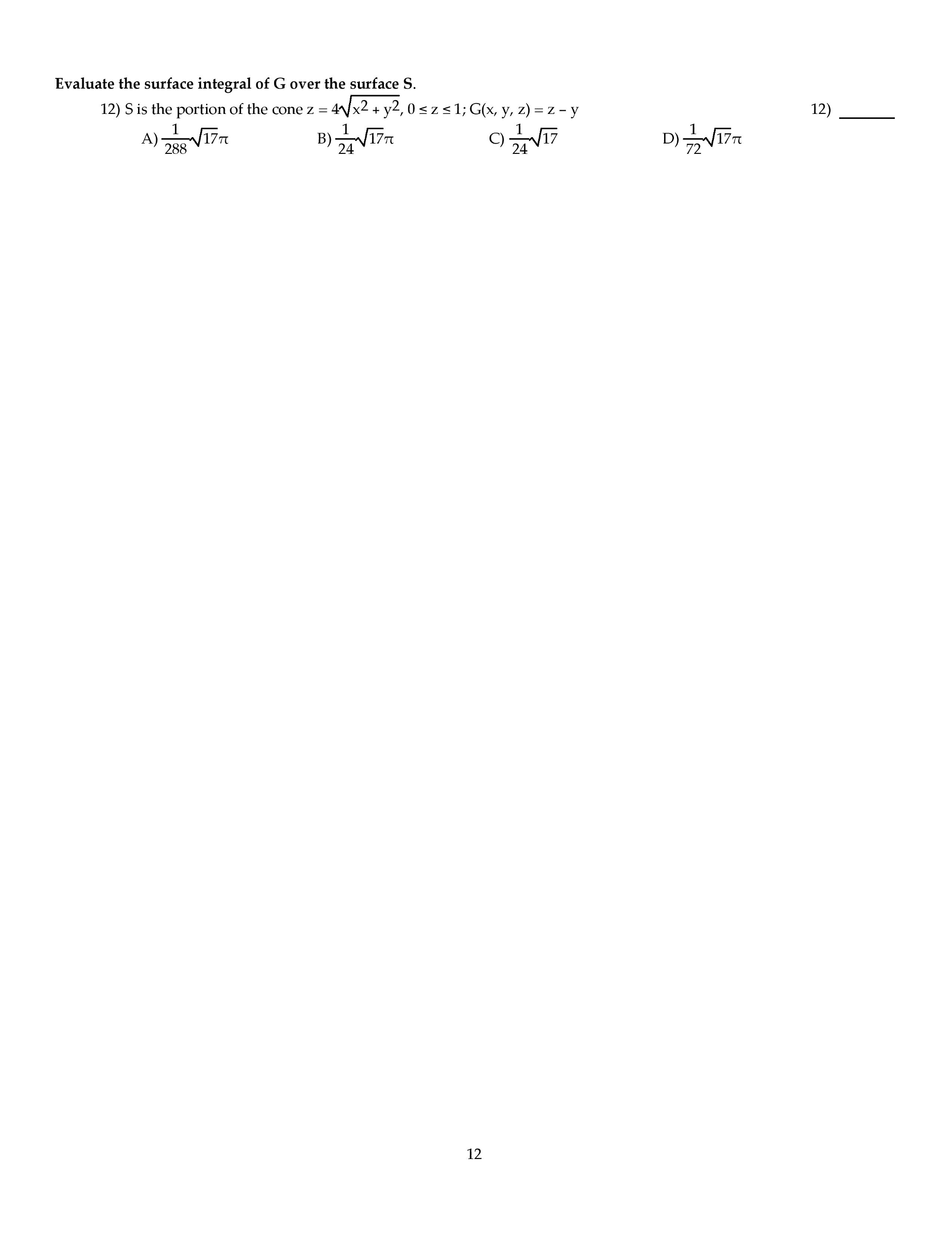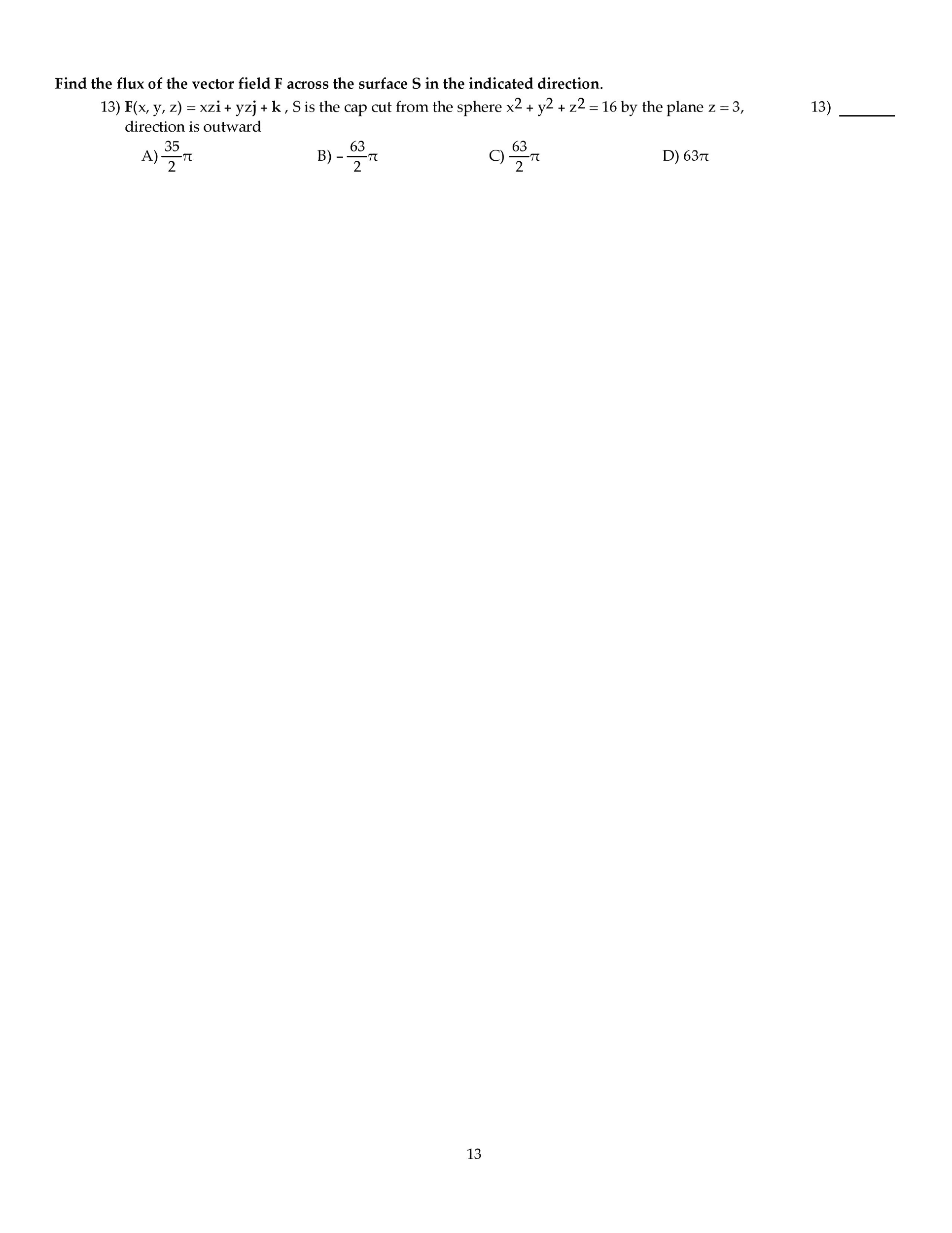Solve all please.
INSTRUCTIONS: There are 15 problems on this exam, and each problem is worth 13 points, plus 5 points for writing down an approximate volume of the planet Earth in cubic miles at the bottomleft corner of page 3, for a total possible 200 points. For this exam, you are allowed to use one 8.5"X11" sheet of notes (both sides, in your own handwriting), pencil, eraser, ruler, scratch paper and calculator. Even though the questions are multiple-choice, you need to show enough work to justify your answer in order to receive full credit. After you have determined the correct solution to each problem, write the letter corresponding to your answer in the appropriate space on the right side of the page AND circle your answer. If your answer does not agree with any of the choices, after double-checking your work, choose option E) and prominently mark your answer (box, circle, underline, etc.). Time limit: Two hours. Attach (i.e. staple) any notecard and scratch paper to the rear of this exam paper. Good luck! MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Solve the problem. The northern third of Indiana is a rectangle measuring 96 miles by 132 miles. Thus, let D = [0, 96] times [0,132]. Assuming that the total annual snowfall (in inches), S(x,y), at (x,y) euro D is given by the function S(x,y) = 60e-0.001 (2x + y) with (x,y) euro D, find the average snowfall on D. 51.14 inches 52.06 inches 51.78 inches 52.44 inches Evaluate the work done between point 1 and point 2 for the conservative field F. Using Green's Theorem, compute the counterclockwise circulation of F around the closed curve C. Evaluate the surface integral of G over the surface S. S is the portion of the cone Find the flux of the vector field F across the surface S in the indicated direction. Using the Divergence Theorem, find the outward flux of F across the boundary of the region D. Integrate the function f over the given region. f(x,y) = 1/ln x over the region bounded by the x-axis, line x = 9, and curvey y = ln x Reverse the order of integration and then evaluate the integral Use a double integral in polar coordinates to find the area of the region specified in polar coordinates. the region inside both r = 7 sin Theta and r = 7 cos Theta Use spherical coordinates to find the volume of the indicated region. the region bounded above by the sphere x2 + y2 + z2 = 25 and below by the cone z = Find the center of mass of the rectangular solid of density (x,y,z) = xyz defined by 0 LE x LE 8, Use the given transformation to evaluate the integral. where R is the parallelogram bounded by the lines y = 8x + 8, y = 8x +9, y = -6x + 2, y = -6x +7 Evaluate the line integral along the curve C. Find the work done by F over the curve in the direction of increasing t.