MATH 240 Final: MATH 240 KSU Finalu14

• School: Kansas State University
• Department: Mathematics
• Course: MATH 240
• Professor: All

Document Summary

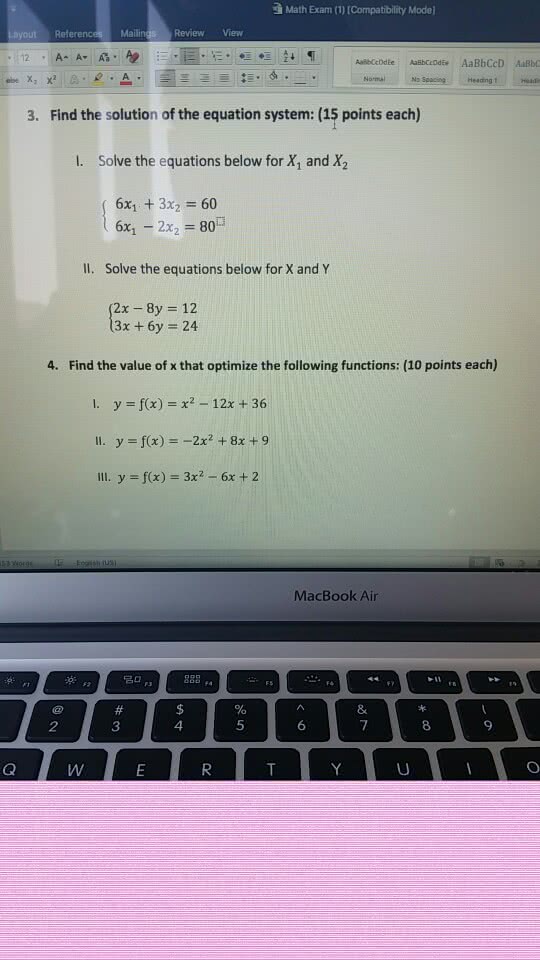
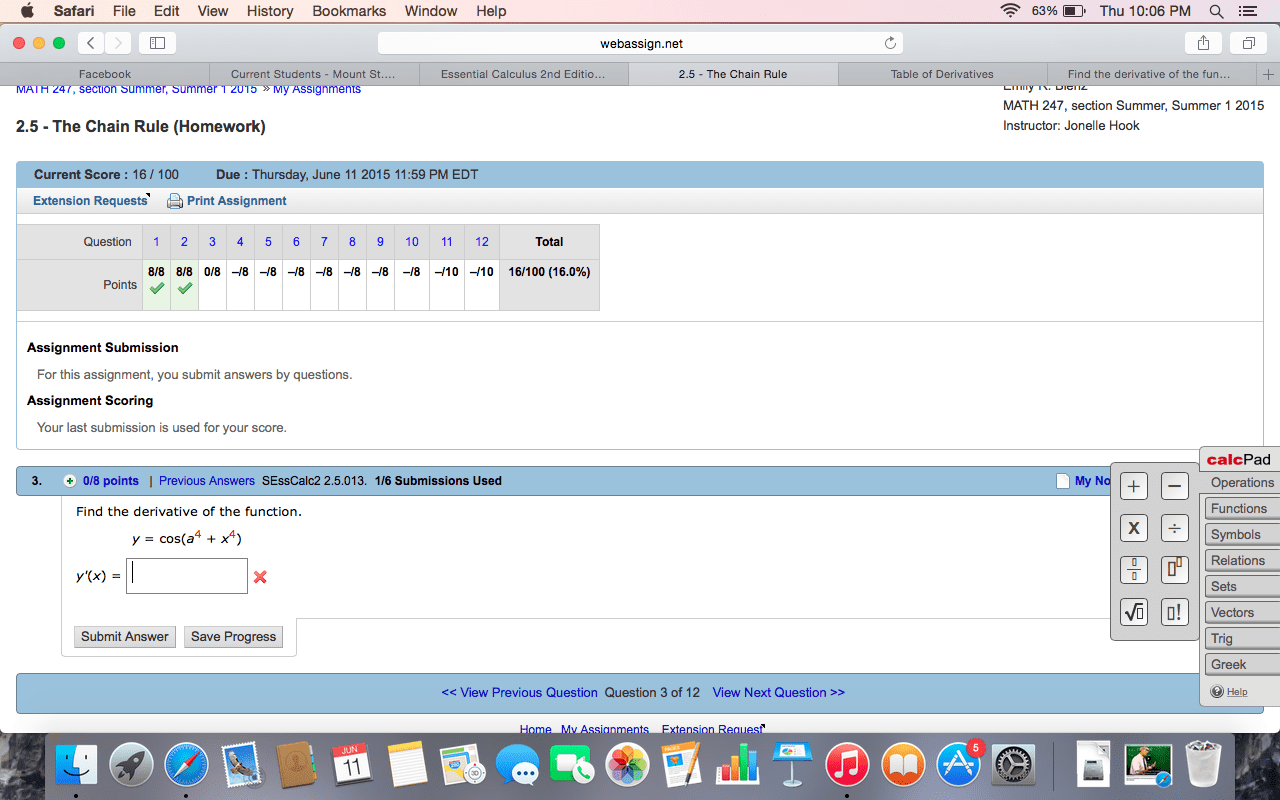
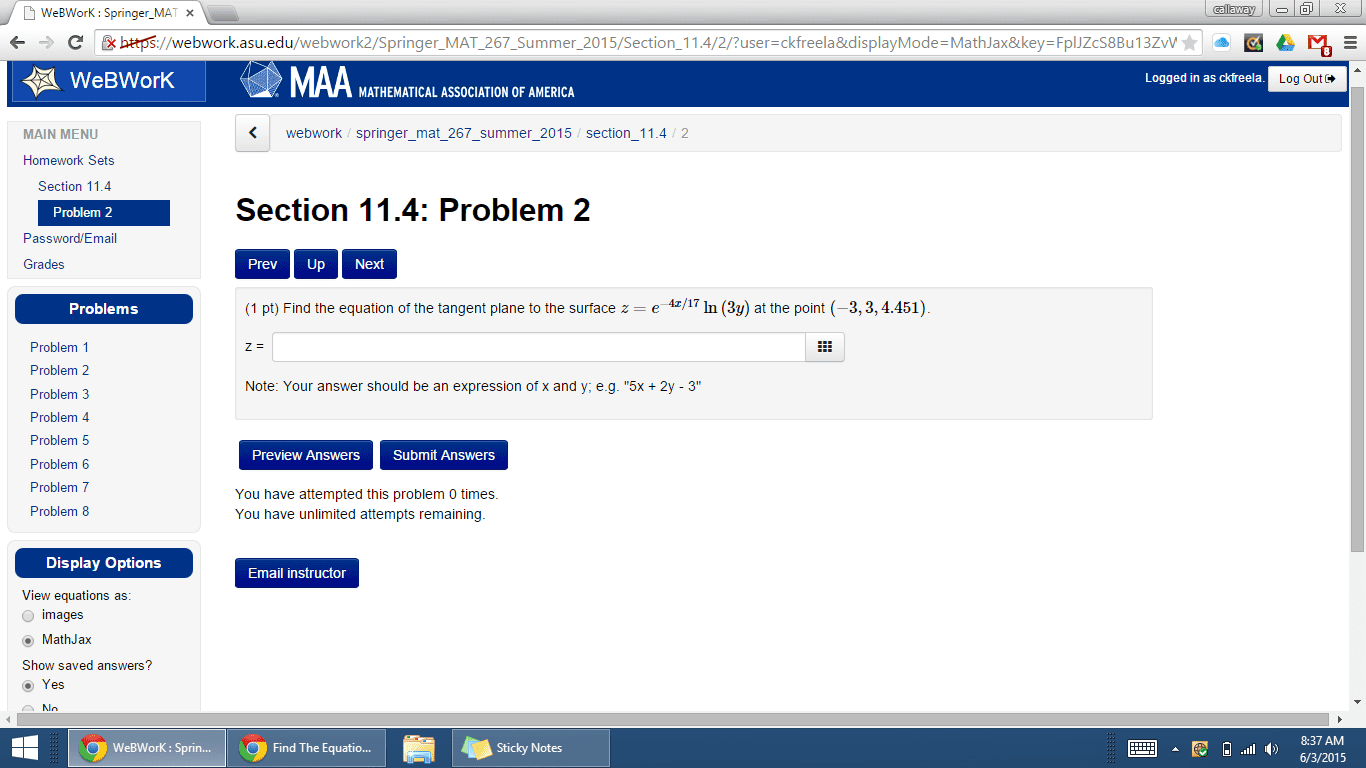
Problem 1. (18 points) find and classify the equilibrium points for the following system of equations: (cid:26) x (t) = x2 y y (t) = y x 2. Problem 2. (20 points) find all the solutions for. Then solve the initial value problem: y + 2xy = 2e. Problem 3. (16 points) use laplace transform to solve the initial value problem: x (t) + 4x(t) = e t x(0) = x (0) = 0. Problem 4. (24 points) use change of variable to solve the euler equation: Then use variation of parameter to solve the corresponding inhomogeneous equation: 2 x y (x) + 7xy (x) + 9y(x) = x. Pn=0 anxn is series solution of the equation, nd the recurrence relation of the. Problem 6. (18 points) for what values of nonnegative , that is, 0, are there in nitely many solutions to the boundary value problem? y + 4 y = 0, y(0) = y(1) = 0.