MATH 3000 Midterm: MATH 331 Mizzou Exam xam1

• School: Mizzou
• Department: Mathematics
• Course: MATH 3000
• Professor: All

Document Summary

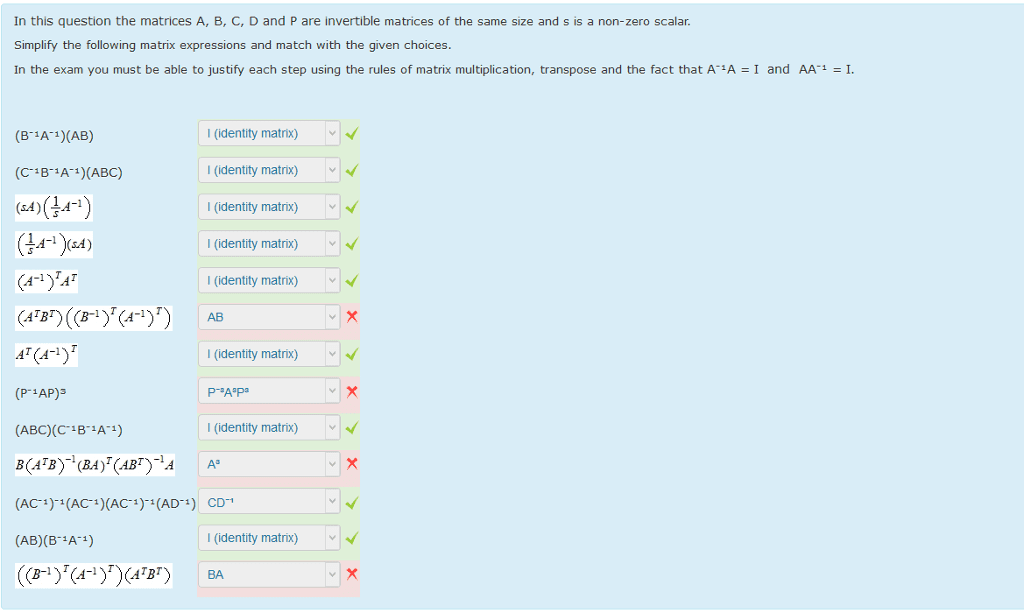
Solutions to exam 3 p( 1)(cid:21) + (cid:20) q(1) p( 1)(cid:21) = l(p). p( 1) + q( 1)(cid:21) = (cid:20) p(1) (p + q)( 1)(cid:21) = (cid:20) p(1) + q(1: a) l(p + q) = (cid:20) (p + q)(1) P( 1)(cid:21) = (cid:20) p(1: ker(l) = {p p5 | l(p) = 0}. Notice that this means that your basis should be elements in p5 (not r5). Say p(x) = a + bx + cx2 + dx3 + ex4. Then p ker(l) if and only if p(1) = p( 1) = 0, so a + b + c + d + e = 0 and a b + c d + e = 0. You thus need to put the matrix (cid:20) 1. You will get (cid:20) 1 0 1 0 1. 0 1 0 1 0(cid:21), thus a = c e and b = d, q( 1)(cid:21) = l(p) + l(q) and. 1 while c, d, and e are free.