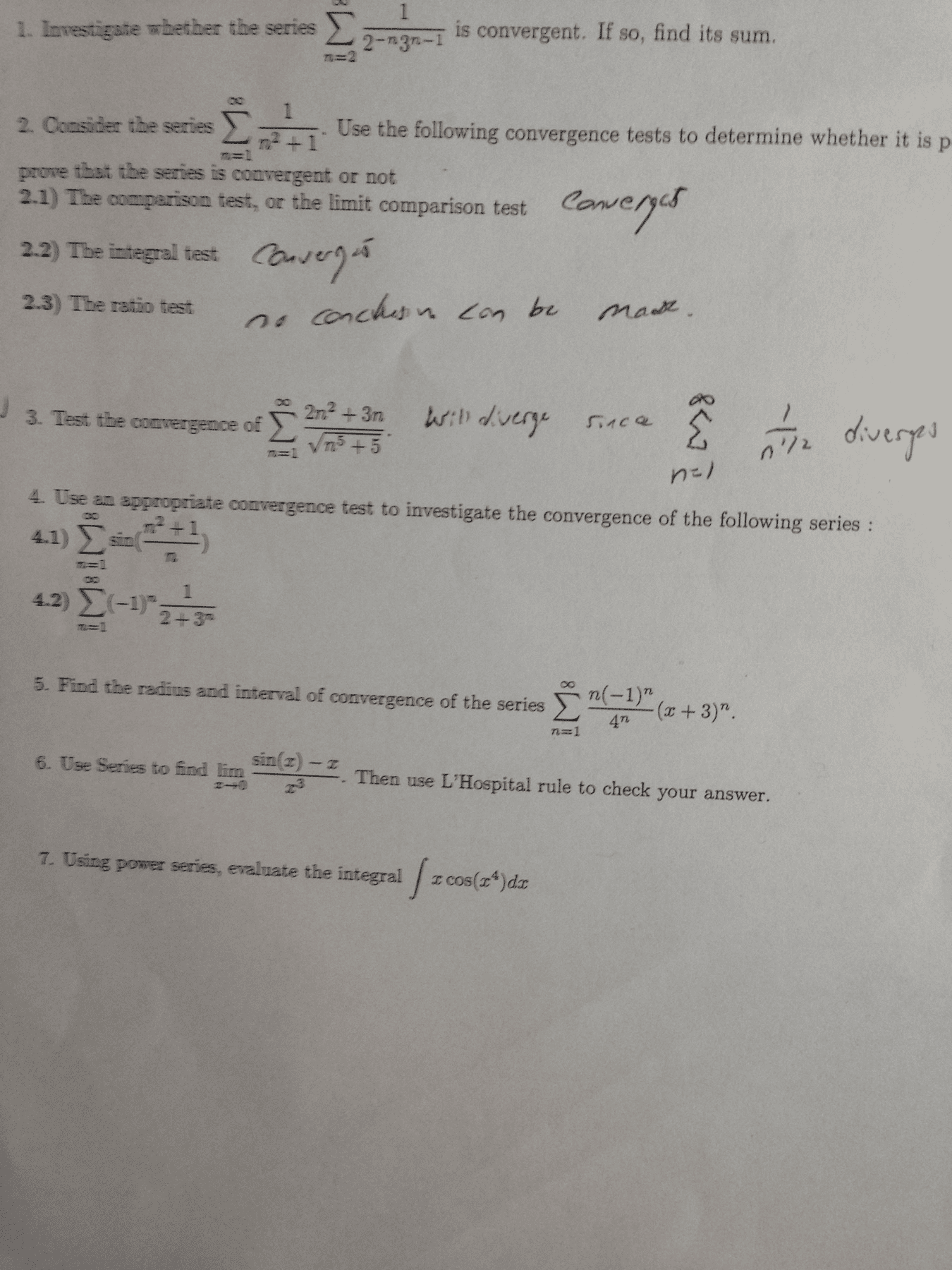MATH-0042 Midterm: w15exam2sol

• School: Tufts University
• Department: Mathematics
• Course: MATH-0042
• Professor: all

Document Summary

Solutions to math 42 second midterm exam: (10 points) (a) compute the interval of convergence of the power series p n=1 radius of convergence, but what happens at the endpoints. ) Use the ratio test: |an+1/an| = |x n2 (n+1)2| |x|, so the radius of convergence is 1. At x = 1 the series is p 1/n2, which converges because it"s a p-series with p > 2; and x = 1 it converges by the absolute convergence test. So it converges exactly for 1 x 1. xn n2 (i. e. , not just the (b) write down the taylor series for e2x around a = 0 (no justi cation is needed). Compute the radius of convergence of this power series, with full justi cation. It converges for all x by the ratio test, so r = . 2nxn n! an | = |2x/(n + 1)|, with limit.