MATH 405 Study Guide - Midterm Guide: Irreducible Polynomial, Unit Circle, Solution Set

• School: University of Maryland
• Department: Mathematics
• Course: MATH 405
• Professor: All

Document Summary

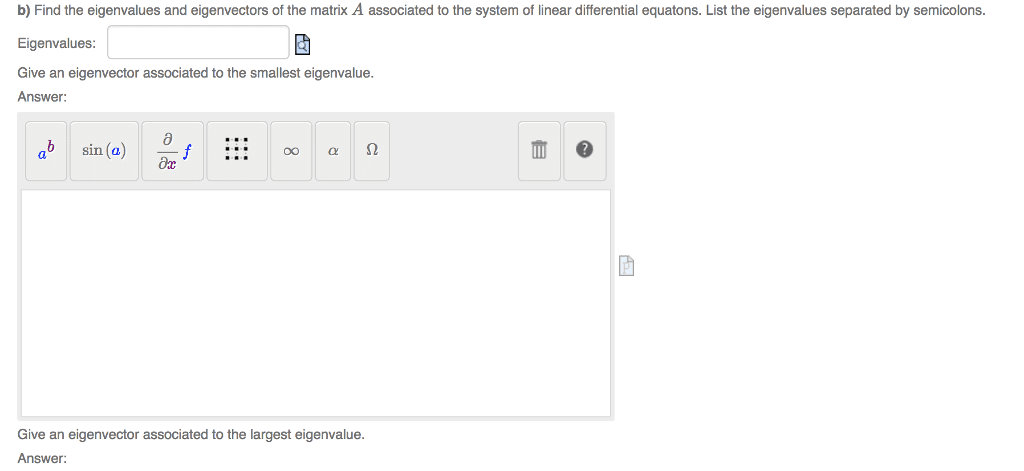
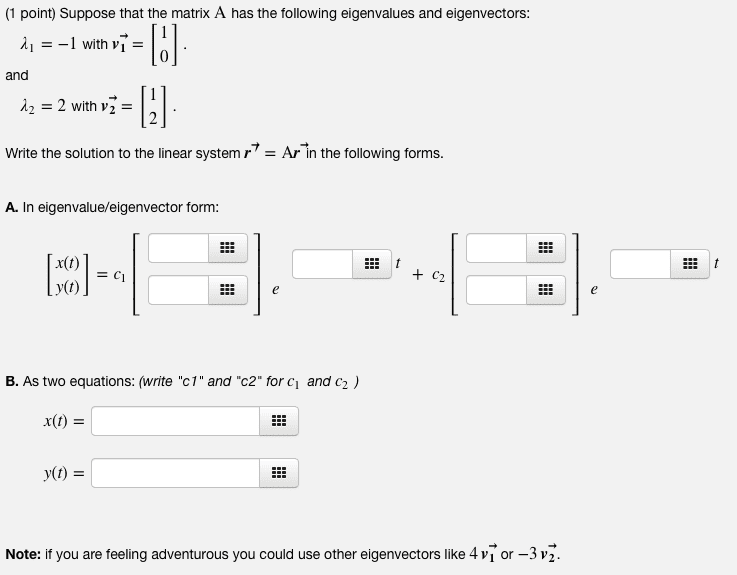
Find the maximum value of q on the unit circle. The maximum value of q on the unit circle is the largest eigenvalue of a, which is (1 + 5)/2: find an orthogonal basis of r2 consisting of eigenvectors for the matrix a = 1 3. The characteristic polynomial of the matrix is x2 3x 7, so the two eigenvalues are. If is an eigenvalue, then an eigenvector for is a nonzero solution x = x1 x2! For each , the solution set is a line, which must be contained in (and therefore equal to) the line which is the set of x such that (1 )x1 + 3x2 = 0. Substituting the two eigenvalues for , we get eigenvectors for the two. These vectors are a basis for r2 and are automatically orthogonal because a is sym- metric: suppose that a is 3 3 with eigenvalues 1, 2 and 2.