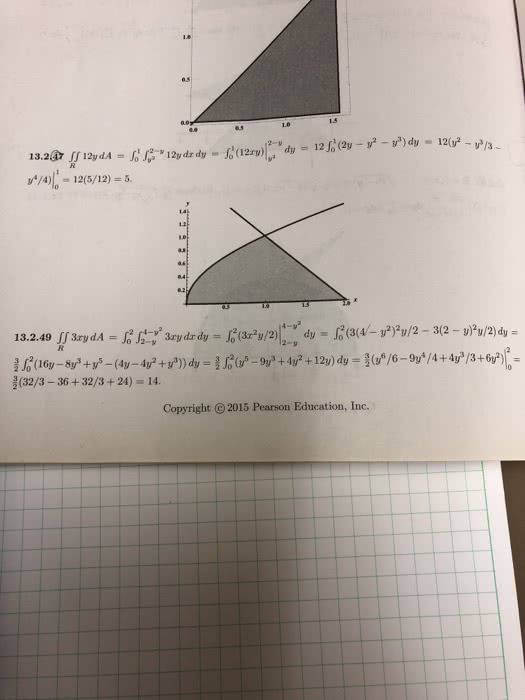
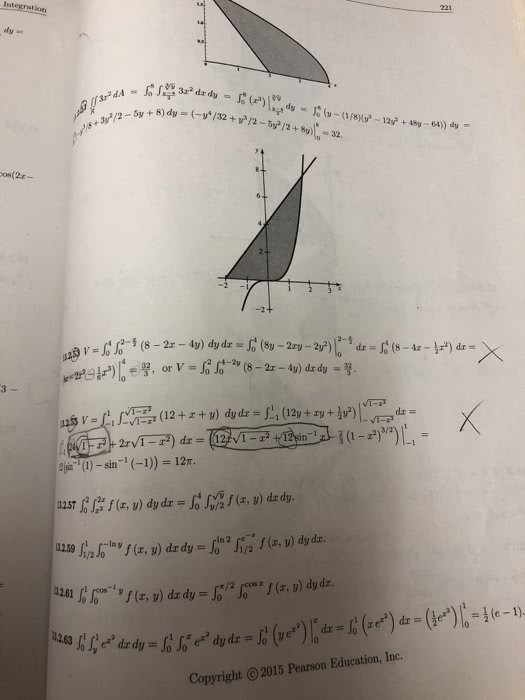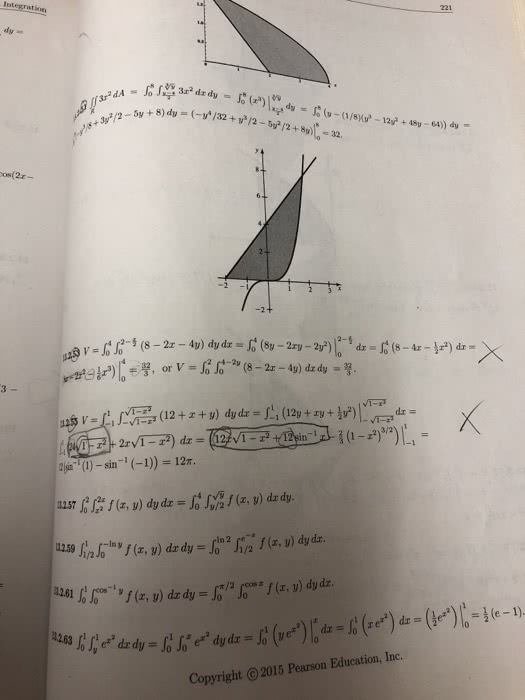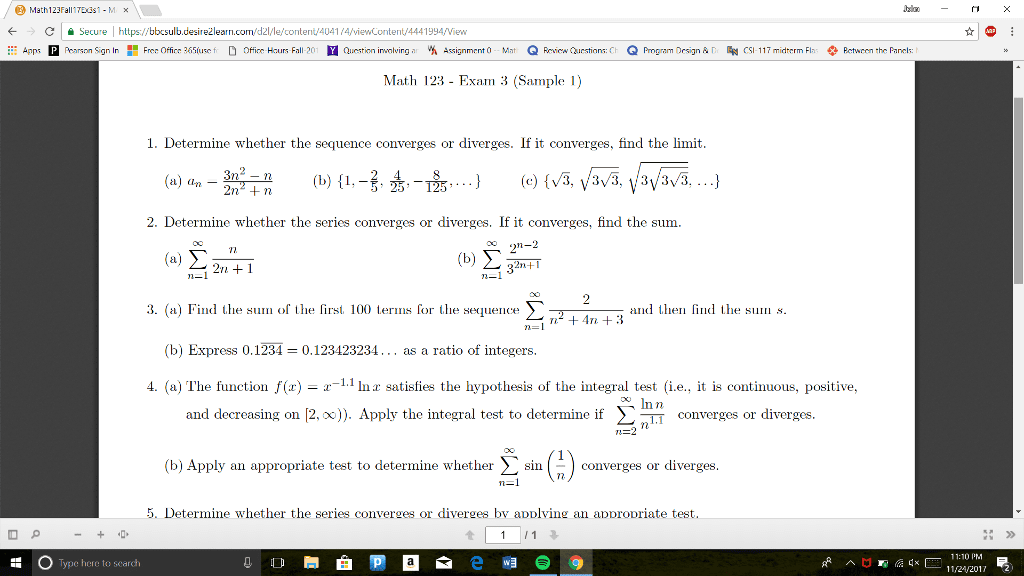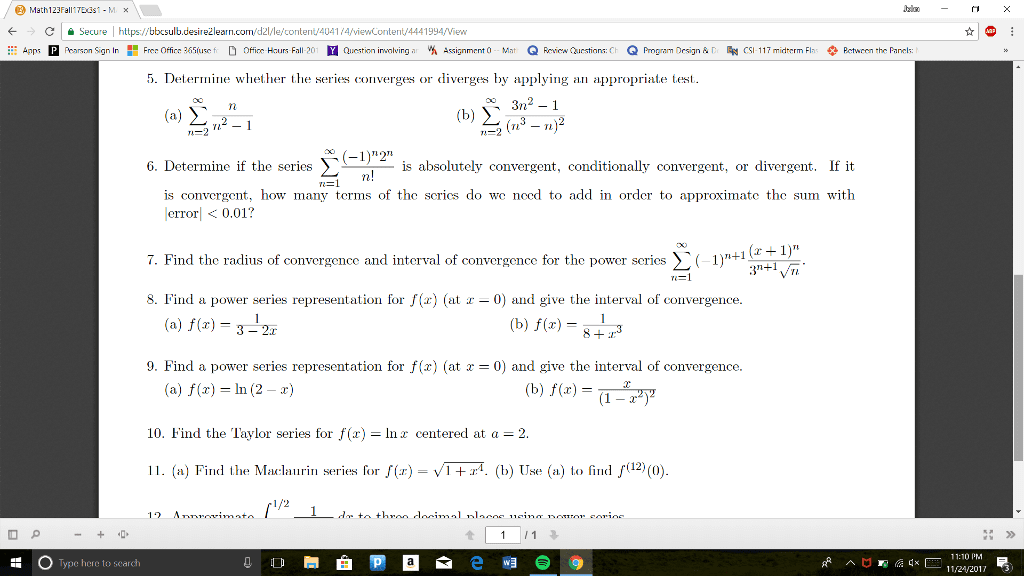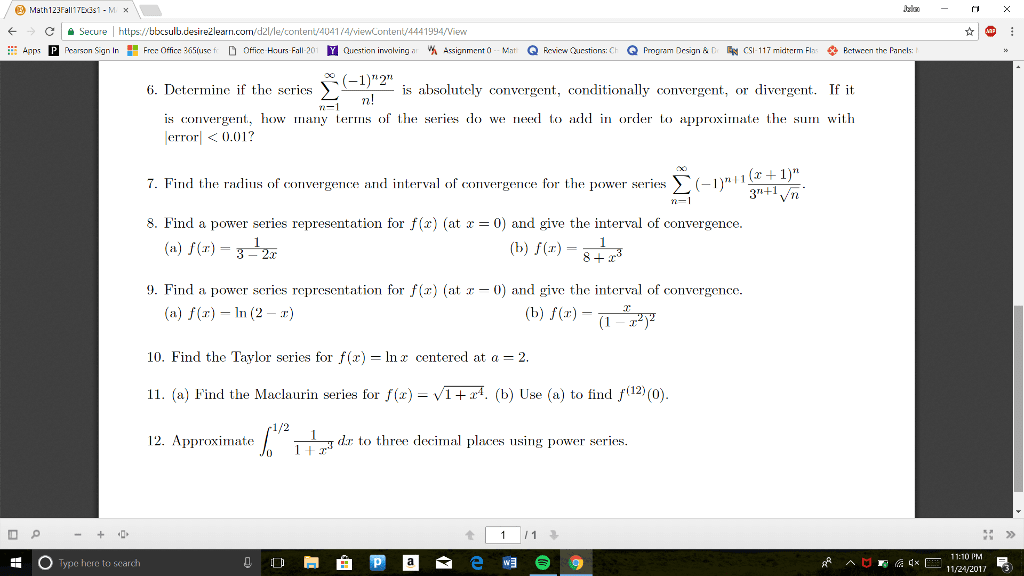MTH 310 Study Guide - Final Guide: Multiple Integral, Multivariable Calculus, Polar Coordinate System

Multivariable Calculus Final Exam Study Guide
12.1: Evaluating Double Integrals
• Volume of solid
The volume of a solid with top & base is found by
. Always have to
sketch the region D to determine the limits of integration. When given equation with , such as
that of a plane, isolate first.
• Type I integrals
A Type I integral is first differentiated with respect to y, holding x is constant. It is then
differentiated like normal integral with respect to x. Note: x can be pulled out since constant.
• Type II integrals
A Type II integral is first differentiated with respect to x, holding y is constant. It is then
differentiated like normal integral with respect to y. Note: y can be pulled out since constant.
• Determining type of iterated integral
If the rectangles are drawn up & down (vertical), evaluate as Type I. If the rectangles are drawn
left & right (horizontal), evaluate as Type II. Some regions can be evaluated both ways, so pick
the easier one to integrate. This is called changing the order of integration. Some can be
broken up into both.
• Volume bounded by plane
If given a function and asked to find the volume of it bounded by the plane, not a region,
you need to find what the region looks like. Do this by finding the points the function intersects
the plane at. For this, set & determine what you get. Usually a circle.
• Properties of double integrals
1. If D is split into two regions, you can sum the two. ,
2.
Recall that can be found by
(or with respect to
y if Type II).
12.3: Double Integrals in Polar Coordinates
• Converting to polar
In replace the following: . To
express in terms of polar coordinates, can go from , depending on where in the
plane the region is. can be anything depending on how far out in the plane the region
goes.
Top:
Bottom:
a b
Left:
Right:
d
c
find more resources at oneclass.com
find more resources at oneclass.com

• Typical integrals to express in polar coordinates
When the area element involves a (part of a) circle, polar is easier or if there’s an that
can be factored out. You can find the area under a curve over a ring (between two circles).
• Formula for conversion
If is continuous on a polar region ,
12.4: Applications of Double Integrals
• Mass
Consider a thin plate in the plane. If is the density of the plate at point , you
can find the mass of the plate. If the density was a constant, . If not, it depends
on the point
• Center of mass
The center of mass is the balance point. If density is’t ostat, hae to fid poit
not just the center of the plate.
13.1: Vector Fields
• Vector field
A vector field in space is a rule which assigns to each point in space a vector
based at . They can also be in the plane.
• Gradient
Gradient is an important example of vector fields. Given
13.2: Line Integrals
• Parameterized Curves
You can parameterize a curve in two ways. It can be written as one function of or as
multiple parametric equations. You will get a range for .
Gie a ure that is’t paraeterized, you a paraeterize it by setting one variable equal to
& writing the other as the given function, replacing the variable with . You will have to check
what the range for is.
The parameterized curve for a circle is
find more resources at oneclass.com
find more resources at oneclass.com
Document Summary
Multivariable calculus final exam study guide (cid:3005: type i integrals, volume of solid. The volume of a solid with top (cid:1878)=(cid:1858)(cid:4666)(cid:1876),(cid:1877)(cid:4667) & base (cid:1830) is found by (cid:1517)(cid:1858)(cid:4666)(cid:1876),(cid:1877)(cid:4667) (cid:1856). Always have to sketch the region d to determine the limits of integration. When given equation with (cid:1878), such as that of a plane, isolate (cid:1878) first. Top: (cid:1877)=(cid:1859)(cid:2870)(cid:4666)(cid:1876)(cid:4667) (cid:3034)(cid:3118)(cid:4666)(cid:3051)(cid:4667) (cid:3034)(cid:3118)(cid:4666)(cid:3051)(cid:4667) (cid:3029) (cid:3029) (cid:1858)(cid:4666)(cid:1876),(cid:1877)(cid:4667) (cid:1858)(cid:4666)(cid:1876),(cid:1877)(cid:4667) (cid:3034)(cid:3117)(cid:4666)(cid:3051)(cid:4667) (cid:3034)(cid:3117)(cid:4666)(cid:3051)(cid:4667) (cid:3028) (cid:3028) A type i integral is first differentiated with respect to y, holding x is constant. It is then differentiated like normal integral with respect to x. Note: x can be pulled out since constant. (cid:1856)(cid:1877)](cid:1856)(cid:1876) (cid:1856)(cid:1877)(cid:1856)(cid:1876: type ii integrals. A type ii integral is first differentiated with respect to x, holding y is constant. It is then differentiated like normal integral with respect to y. Note: y can be pulled out since constant. (cid:3117)(cid:4666)(cid:3052)(cid:4667) (cid:3030) (cid:1856)(cid:1876)](cid:1856)(cid:1877) d c: determining type of iterated integral a b.