MTH 162 Final: MTH 162 University of Rochester pr Final Fall 05

• School: University of Rochester
• Department: Mathematics
• Course: MTH 162
• Professor: All

Document Summary

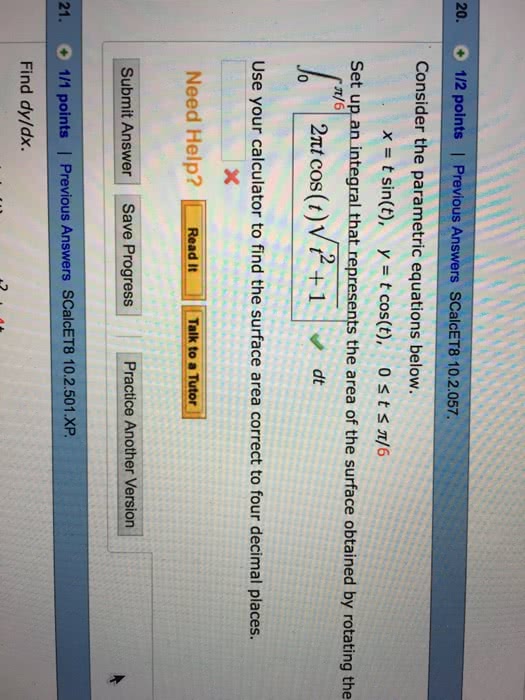
Part a: (30 points) (a) (10 points) calculate (b) (10 points) calculate (c) (10 points) calculate. 1 x 2: (12 points) a hemispherical reservoir is lled with water. The radius of the hemisphere is r ft. 1: (10 points) make a rough sketch of the graph of r = sin(2 ). Set up an integral which calculates the area of one petal of the graph of r = sin(2 ): (24 points) match the equations with the graphs. The equations are given on the next page. Record your answers on the answer sheet, not on this sheet. 4: (11 points) find the radius of convergence for the following power series. 2n xn: (11 points) find the taylor polynomial for, (12 points) suppose that. T2(x) = c0 + c1x + c2x2 f (x) = 1 + ex. f (5)(x) = cos2 x ex + 3 (a) (6 points) find a number m such that.