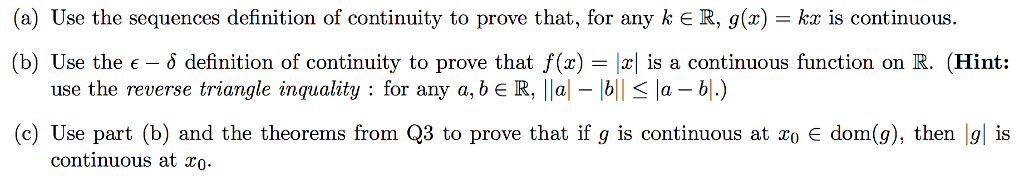MATH 3770 Final: MATH 3770 Iowa M55OldFinals0206
Document Summary
Old finals theorems or by providing a proof. 22m:55, section a-old final exams, 2006: a. Determine whether lim x!0(cid:12)(cid:12)sin 1 x(cid:12)(cid:12) exists or not. Justify your answer by applying x!5(cid:0)x2 (cid:0) 3x + 1(cid:1) = 11 directly from the de nition of the limit lim: prove that (8"9(cid:14):::): x. R at a point c 2 i: prove the following (theorem 21. 12). R; where i and j are intervals in r. if f is continuous at c 2 i and g is continuous at f (c); then g (cid:14) f : i ! R is continuous at c: let h(x) =(cid:26) x2 (cid:1) cos 1 if x 6= 0 if x = 0. Prove your assertion: prove the following (theorem 25. 7b). R; where i is an interval in r. if both f and g are differentiable at c 2 i, then f + g : i ! R is differentiable at c and (f + g)0(c) = f.