ENGR2000 Lecture Notes - Lecture 2: American Broadcasting Company, Ya Sin, Sluice

2nd-Year Fluid Mechanics, Faculty of Science & Engineering, Curtin University
ENGR2000: FLUID MECHANICS
For Second-year Chemical, Petroleum, Civil & Mechanical Engineering
FLUID MECHANICS LECTURE NOTES
CHAPTER 2: HYDROSTATICS
This chapter is concerned with the effect of fluids when flow is absent - hence
the name hydro(water∗1)-statics(forces balanced - hence, no acceleration). In
hydrostatics it is the gravitational forces on the bulk of fluid that create the
pressure in the fluid; in a later chapter we will see that fluid flow affects this
pressure.
Hydrostatics is very important in Engineering because the hydrostatic forces
in fluids can create large forces that act on structures - for example the fluid
force on a dam due to the reservoir that it holds. A knowledge of these forces
then permits the appropriate design of the structure upon which they act.
We will also see that hydrostatic forces are essentially responsible for the
capability of objects, such as ships, to float in a fluid medium. (And, hot-air
balloons to float in air.) This aspect of hydrostatics is called buoyancy and
its fundamentals are covered in this chapter.
2.1 Hydrostatic pressure
We first wish to quantify hydrostatic pressure in a fluid. We know that, for
example, a scuba diver experiences increasing pressure the deeper that s/he
dives. The simple reason for this is that the deeper s/he goes, the greater the
weight of water there is above him applying a force (per unit area) to his/her
body. This type of approach leads us to derive an expression for hydrostatic
pressure.
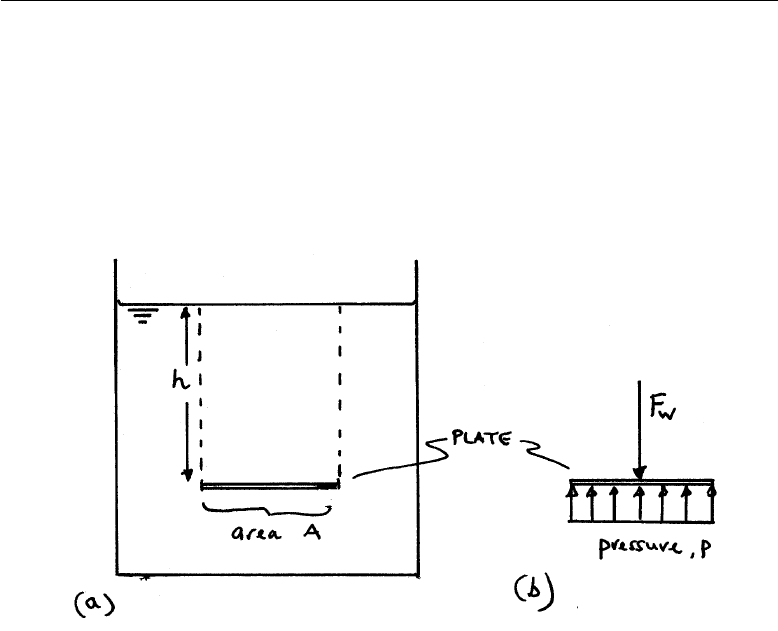
Consider a tank of fluid which contains a very thin plate of (neutrally buoy-
ant) material with area A. This situation is shown in Fig. 2.1a. If the plate
1∗However, many of the principles also apply to gases - the discipline is so called because
the fluid forces are very large for liquids which have a high density as compared to gases
which have relatively low densities.
Chapter 2 −Page 1
find more resources at oneclass.com
find more resources at oneclass.com
2nd-Year Fluid Mechanics, Faculty of Science & Engineering, Curtin University
is in equilibrium (it does not start to move), then the forces on it must be
balanced. On the top side of the plate acts the weight of the fluid, with den-
sity ρ, above it in the downward direction. Because it does not accelerate,
there must be a force acting upwards on the underside of the plate - this is
the effect of the hydrostatic pressure acting on the plate.
FIGURE 2.1: (a) Thin plate in a fluid, (b) Free-body diagram for the plate
The weight of the fluid above the plate is
FW= density ×volume of fluid above ×g
=ρg(Ah) (2.1)
Balancing this is the hydrostatic pressure, p, acting over the area, A, of the
underside of the plate depicted in Fig 2b. Balancing the two forces yields
pA =ρgAh
cancelling Agives the expression for the hydrostatic pressure as
p=ρgh in N/m2or Pa (Pascals) (2.2)
noting that his the vertical depth. You can now see the relationship between
hydrostatic pressure and gravitational forces. We have derived Eqn. 2.2 for
a particular depth, h. We could derive it for any depth, y, where yis a
downward coordinate from the liquid surface, giving the formula p=ρgy.
Chapter 2 −Page 2
find more resources at oneclass.com
find more resources at oneclass.com
2nd-Year Fluid Mechanics, Faculty of Science & Engineering, Curtin University
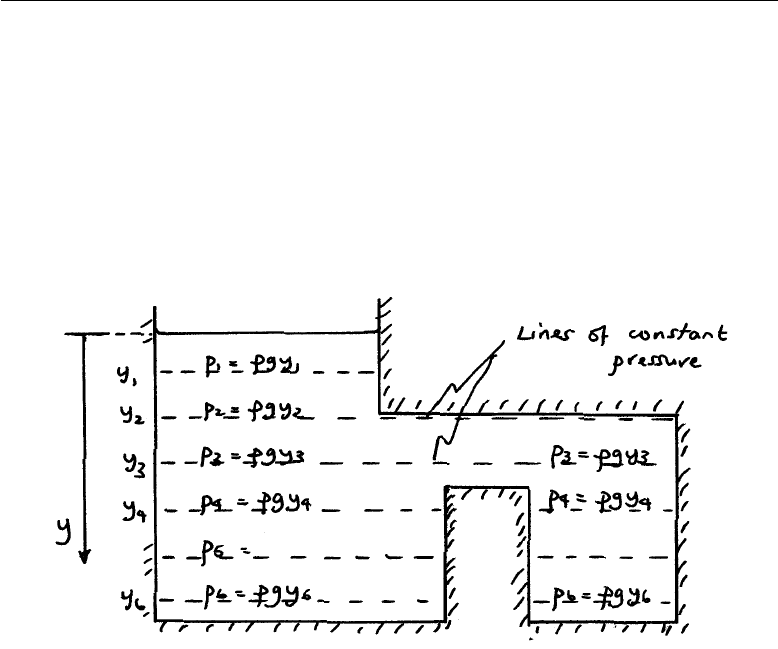
We now note that this pressure is the same at all points in the fluid with the
same vertical location (y-coordinate)) for an interconnected body of fluid.
To illustrate this, lines of constant pressure are shown in Fig. 2.2.; i.e. a
plot of p=ρgy for different values of y. The resulting diagram represents
the pressure field in the fluid. Note that these lines are all horizontal
because there is no variation with the horizontal coordinate, x, in the pressure
formula.
FIGURE 2.2: The pressure field in an interconnected body of static fluid
If we evaluated the expression above, we would not find the total pressure
acting on the plate. This is because, using the same arguments, there is a
column of atmospheric air above the water in the tank and this presses down
on the water which, in turn, transmits the additional pressure onto the plate
. If we denote the air pressure at the liquid surface PA(again, in N/m2),
then the total pressure at a depth his
pabs =ρgh +PA(2.3)
This is called the absolute pressure whilst the pressure of Eqn. 2.2 is called
the gauge pressure, i.e. the pressure relative to atmospheric pressure.
In the derivation above, we can also see that the downward force on the
upper side of the plate also has an intensity, or pressure, given by ρgh. In
fact the effect of the fluid loading above results in a hydrostatic pressure,
acting downwards, on the upper side of the plate.
So far, it seems that pressure only acts in the vertical direction. We now show
that at any point in the fluid, the same pressure actually acts in a direction
Chapter 2 −Page 3
find more resources at oneclass.com
find more resources at oneclass.com
Document Summary
For second-year chemical, petroleum, civil & mechanical engineering. This chapter is concerned with the e ect of uids when ow is absent - hence the name hydro(water 1)-statics(forces balanced - hence, no acceleration). In hydrostatics it is the gravitational forces on the bulk of uid that create the pressure in the uid; in a later chapter we will see that uid ow a ects this pressure. Hydrostatics is very important in engineering because the hydrostatic forces in uids can create large forces that act on structures - for example the uid force on a dam due to the reservoir that it holds. A knowledge of these forces then permits the appropriate design of the structure upon which they act. We will also see that hydrostatic forces are essentially responsible for the capability of objects, such as ships, to oat in a uid medium. (and, hot-air balloons to oat in air. )

