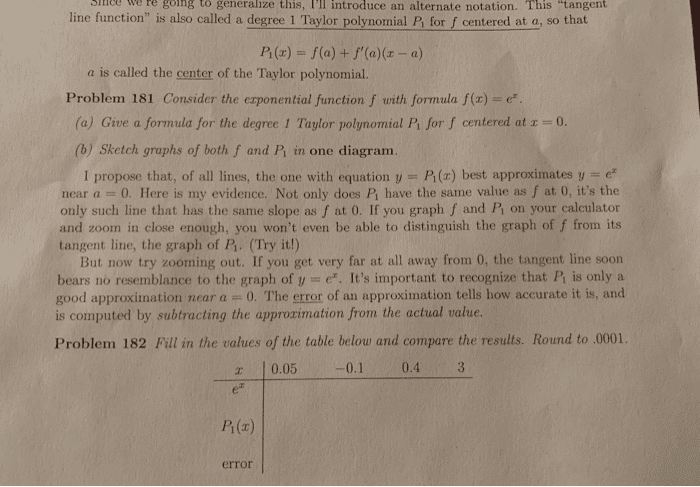MATH 140 Lecture Notes - Lecture 2: Algebraic Function, Phenylalanine, Cubic Function

• School: McGill University
• Department: Mathematics & Statistics (Sci)
• Course: MATH 140
• Professor: Ewa Duma

Document Summary

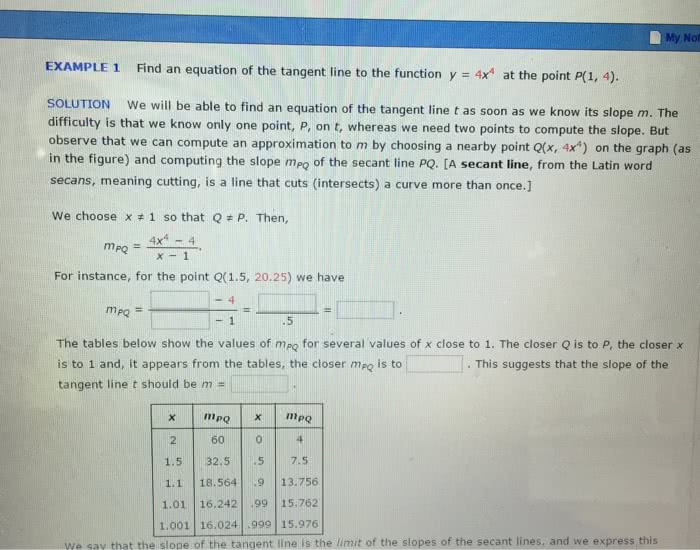
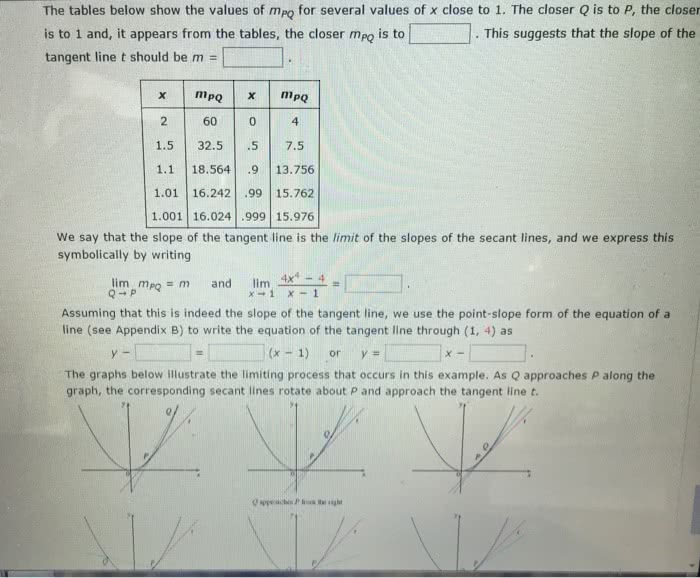
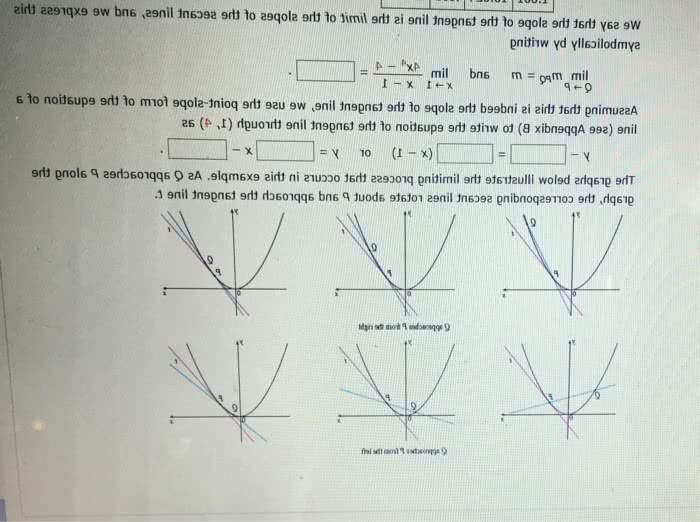
A characteristic feature of linear functions is that they grow at a constant rate. For and a table of sam- increases by 0. 3. , namely 3, can: note that m is the slope of the line, the value b is the y-intercept of the line instance, figure 2 shows a graph of the linear function ple values. Notice that whenever x increases by 0. 1, the value of f x be interpreted as the rate of change of y with respect to x. increases three times as fast as x. Thus the slope of the graph f x 3x 2 f x y 3x 2. We therefore predict that the prediction is somewhat risky because it involves a time quite remote from our observations. level will exceed 400 ppm by the year 2019. M x f x 3x 2. V (a) as dry air moves upward, it expands and cools.