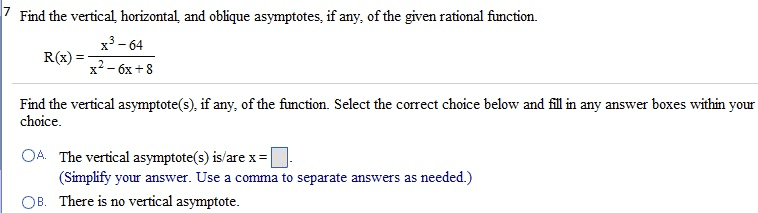
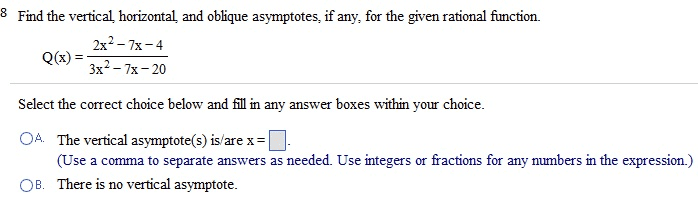
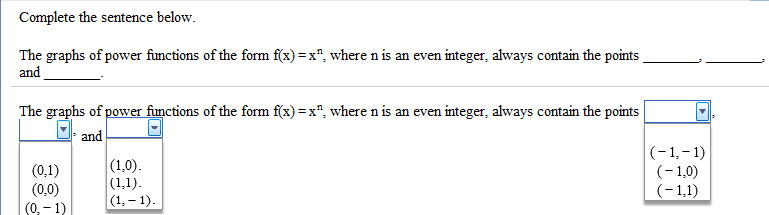What are the answers for all of these questions? I am confused on how to solve for these.
1.
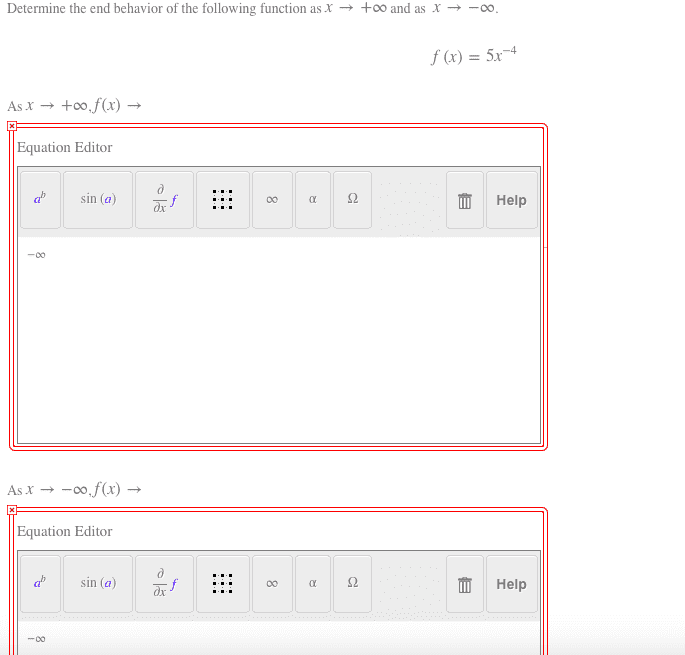
2.

3.

4.
Determine the end behavior of the following function as x â +oo and as X â-00. f(x) = 5x-4 As x â +00,f(x) â Equation Editor | sin (a) x/ è¡Help -00 As X â -00,f(x) â Equation Editor d' sin (a) Help -00
XYour answer is incorrect. Try again. Link to question with no attempts available What families does the function 1(x) = Assume a, b and c are positive constants. Select all that apply. ( )" belong to? Power Rational O Exponential Polynomial
Assume/x) is continuous on an interval around x = 0, except possibly at x = 0. What does the table of values suggest as the integer value of lim f(x)? x 1-0. I -0.01 | 0.01 | 0.1 ТР8.987P8.999|98.999 8.987 lim f(x) seems to be equal to 99 Does the limit definitely have this value? Select all the options that apply Yes, because the function is continuous on an interval around x = 0. Yes, the table shows this is the limit with certainty O No, we do not know the limit or sure because for values of Ï c se to 0 different from those the table the va a eso c m ght not approach the given value. O No, the limit may not exist, even though the table seems to hint it does No, the function could be approaching, for example, 99.00001 or 98.9999 Yes, the table indicates that for values of x close to O different from those in the table, the values of f(x) will approach the given value.
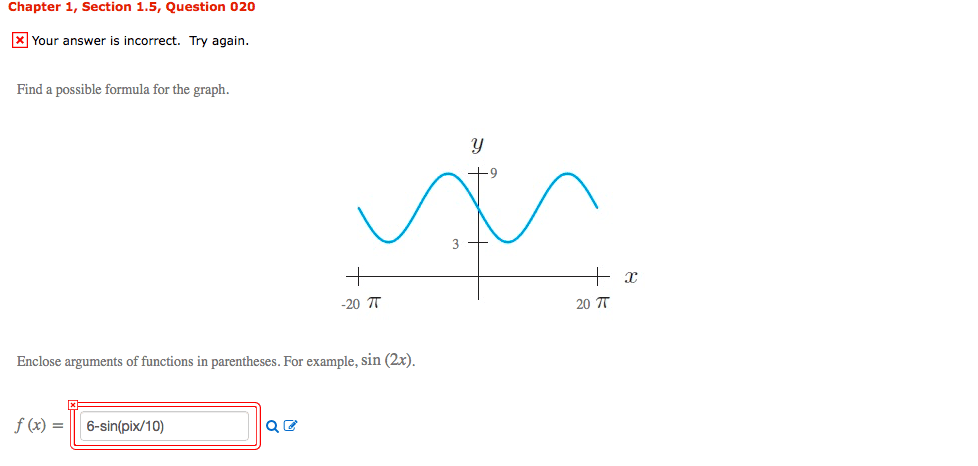
Chapter 1, Section 1.5, Question 020 Your answer is incorrect. Try again. Find a possible formula for the graph -20 Ï 20Ï Enclose arguments of functions in parentheses. For example, sin (2x) f(x)=1 6-sin(pix/10)
Show transcribed image text Determine the end behavior of the following function as x â +oo and as X â-00. f(x) = 5x-4 As x â +00,f(x) â Equation Editor | sin (a) x/ è¡Help -00 As X â -00,f(x) â Equation Editor d' sin (a) Help -00
XYour answer is incorrect. Try again. Link to question with no attempts available What families does the function 1(x) = Assume a, b and c are positive constants. Select all that apply. ( )" belong to? Power Rational O Exponential Polynomial
Assume/x) is continuous on an interval around x = 0, except possibly at x = 0. What does the table of values suggest as the integer value of lim f(x)? x 1-0. I -0.01 | 0.01 | 0.1 ТР8.987P8.999|98.999 8.987 lim f(x) seems to be equal to 99 Does the limit definitely have this value? Select all the options that apply Yes, because the function is continuous on an interval around x = 0. Yes, the table shows this is the limit with certainty O No, we do not know the limit or sure because for values of Ï c se to 0 different from those the table the va a eso c m ght not approach the given value. O No, the limit may not exist, even though the table seems to hint it does No, the function could be approaching, for example, 99.00001 or 98.9999 Yes, the table indicates that for values of x close to O different from those in the table, the values of f(x) will approach the given value.
Chapter 1, Section 1.5, Question 020 Your answer is incorrect. Try again. Find a possible formula for the graph -20 Ï 20Ï Enclose arguments of functions in parentheses. For example, sin (2x) f(x)=1 6-sin(pix/10)