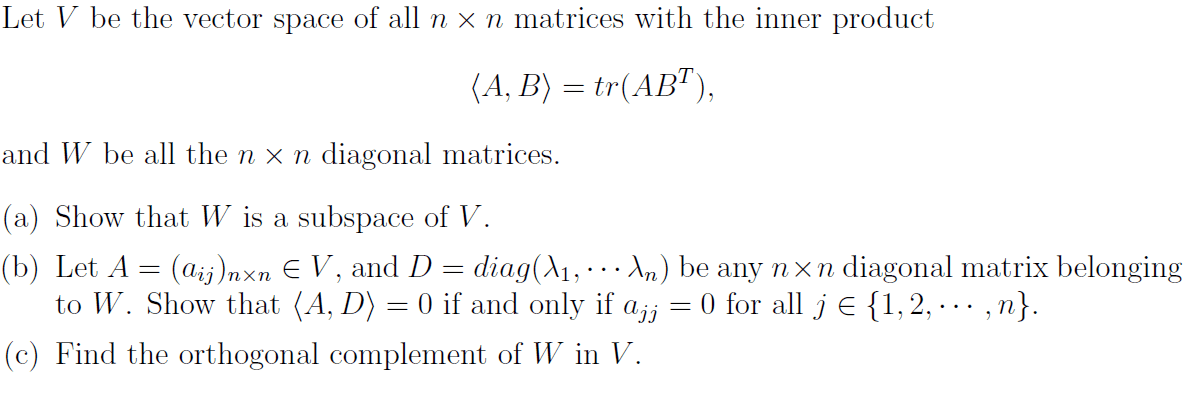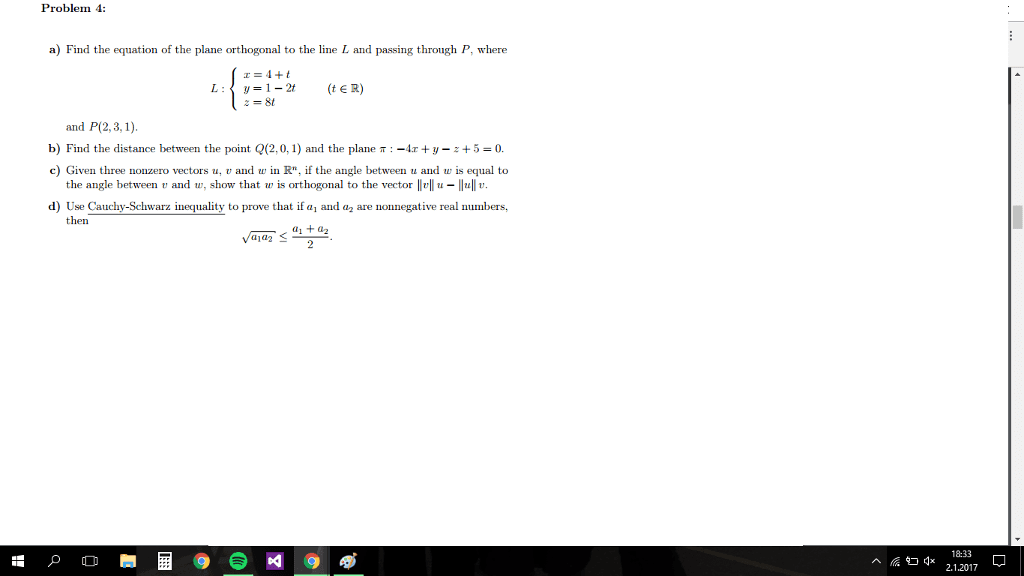MATH125 Lecture Notes - Lecture 37: Orthogonal Complement, Orthogonal Matrix

8
MATH125 Full Course Notes
Verified Note
8 documents
Document Summary
Proof. (a) q 1 = qt is orthogonal. (b) 1 = det i = det(qt q) = det qt det q = (det q)2, so that det q = 1. (c) if v is an eigenvector with eigenvalue , then ||v|| = ||qv|| = || v|| = | |||v|| so that | | = 1. (d) (q1q2)t q1q2 = qt. Rn is orthogonal to w , if v is orthogonal to every vector in w . The set of all vectors that are orthogonal to w is called the orthogonal complement of w , denoted w . W = {v in rn : v w = 0 for all w in w }. Let w be a subspace of rn: w is a subspace of rn, (w ) = w , w w = {0}, if w is spanned by vectors w1, .