MATH125 Lecture Notes - Lecture 25: Linear Map, Linear Algebra, Novella

• School: University of Alberta
• Department: Mathematics
• Course: MATH125
• Professor: Nikita

Document Summary

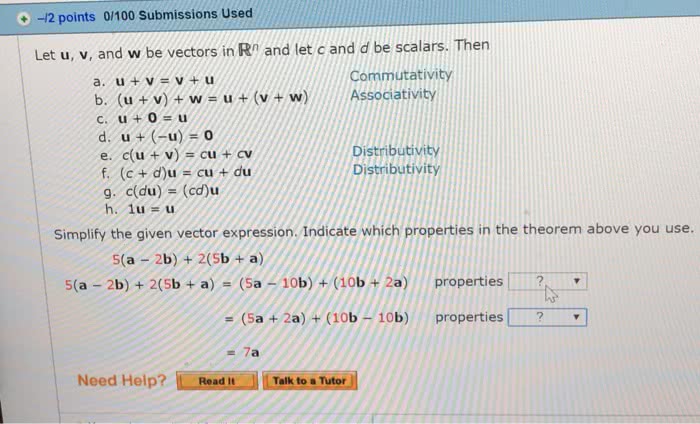
Consider the above transformation t : r2 r3 given by v2 ] av = . Indeed, let u, v be two vectors in r2. Then t (u + v) = a(u + v) = au + av = t (u) + t (v). T (cv) = a(cv) = c(av) = ct (v). In the above example there is nothing special in size 3 2 of the matrix a. Let a be a matrix of size m n. then the transformation. Ta : rn rm given by v ta(v) = av is a linear transformation. Let f : r2 r2 be the transformation that sends each point to its re ection in the x-axis. Let us show that it is a linear transformation. By construction, the transformation f sends the point (x, y) to the point (x, y). F ([ x y ]) = [ x.