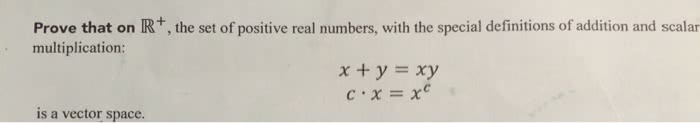By using the definition of a vector space
How do I prove this?
Let V be a nonemp an addition operation and a scalar multiplication operation with scalars V a vector space over F, provided the following ten pty set (whose elements are called vectors) on which are defined in F. We call conditions are satisfied: AL. Closure under addition: For each pair of vectors u and v in V, the sum u under addition: For each pair of vectors u and v in V, the sumu+v is also in V. We say that V is closed under addition. 2. Closure under scalar multiplication: For each vector v in V and each scalar k n F, the scalar multiple kv is also in V. We say that V is closed under scalar multiplication A3. Commutativity of addition: For all u, v V, we have u+v=v+u. A4. Associativity of addition: For all u, v, w e V, we have (u + v) + w = u + (v + w). A5. Existence of a zero vector in V: In V there is a vector, denoted 0, satisfying v+0=v, for all v E V. A6. Existence of additive inverses in V: For each vector v In V, there is a vector denoted -V, in V such that v+1-v) = 0. A7. Unit property: For all veV Iv=v. A8. Associativity of scalar multiplication: For all v e V and all scalars r, sEF. (rs)vr(sv). A9. Distributive property of scalar multiplication over vector addition: For all u V E V and all scalars r EF r(u + v) = ru + rv. A10. Distributive property of scalar multiplication over scalar addition: For all v e V and all scalars r,SEF (r+s)v = rv + sv.