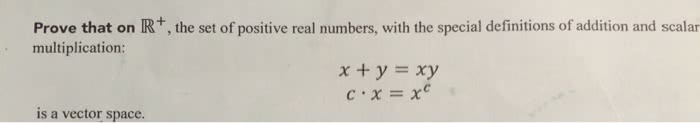MATH136 Lecture Notes - Coordinate Vector, Row Echelon Form, Elementary Matrix

• School: University of Waterloo
• Department: Mathematics
• Course: MATH136
• Professor: Eddie Dupont

Document Summary

Linear algebra (l. a. ) is the study of vector spaces, where vector space is a set of stuff where each elements of the set is called a vector. Note: vectors are not necessarily a column of numbers", rather, column of numbers" are an example of vector in a particular vector space. ] with for , the set of all possible is called . An individual with is called a vector in . Note: it will be sometimes useful to visualize the vectors t as points in a cartesian system (especially and ). The two operations of vectors are called vector addition, and scalar multiplication, which you are free to make it totally whacky. For now we create the intuitive" operations as follows. ] , and c is scalar. If the above properties hold, then the set is called a vector space, and the elements are called vectors.