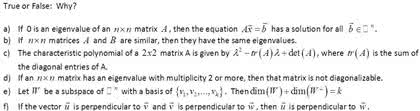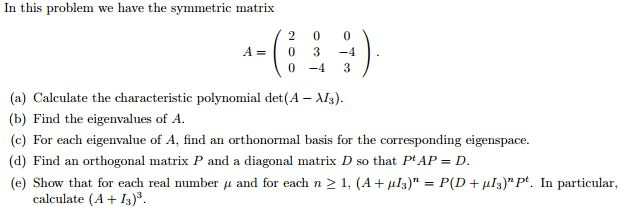MATH136 Lecture Notes - Invertible Matrix, Algebraic Equation, Triangular Matrix

• School: University of Waterloo
• Department: Mathematics
• Course: MATH136
• Professor: Robert Sproule

Document Summary

Wednesday, march 26 lecture 32 : eigenvalues of a matrix. Concepts: definition of eigenvalue of a matrix, definition of the characteristic polynomial of a square matrix a, find the eigenvalues of a matrix, recognize some important properties of characteristic polynomials of a matrix a: The eigenvalues of a triangular matrix are the elements on its diagonal. The number 1 = 0 is an eigenvalue of a if and only if det(a) = 0. The two matrices a and at have the same characteristic polynomial and hence the same eigenvalues. Similar matrices have the same characteristic polynomial (c = b-1ab). The matrices ab and ba have the same characteristic polynomial. 32. 1 definitions let a be a square n n matrix. Let be a variable over (the real numbers). Then det(a i) is a polynomial in . (verify this for 2 2 and 3 3 matrices. )