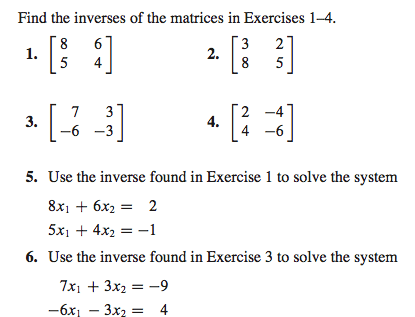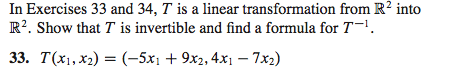MATH136 Lecture Notes - Elementary Matrix, Mathematical Induction, Natural Number

• School: University of Waterloo
• Department: Mathematics
• Course: MATH136
• Professor: Robert Sproule

Document Summary

Wednesday, march 19 lecture 29 : determinants of elementary matrices. 29. 1 theorem suppose a and b are both n n matrices. The proof of a cri b implies det b = c det a is easily obtained by computing det b by expanding b along row ri. The proofs of a pij b implies det b = det a and a cri + rj b implies det b = det a can both be done by induction. To illustrate how this is done we prove. A cri + rj b implies det b = det a . Base case: let a be the 2 2 matrix whose first row is (a, b) and second row is (c, d). Let let a* be the 2 2 matrix whose first row is (kc + a, kb+ d) (obtained by the ero, kr2 + r1) and second row is (c, d).