MATA32H3 Lecture Notes - Lecture 8: Riemann Sum, Marginal Revenue, Antiderivative

• School: UTSC
• Department: Mathematics
• Course: MATA32H3
• Professor: Xiamei Jiang

Document Summary

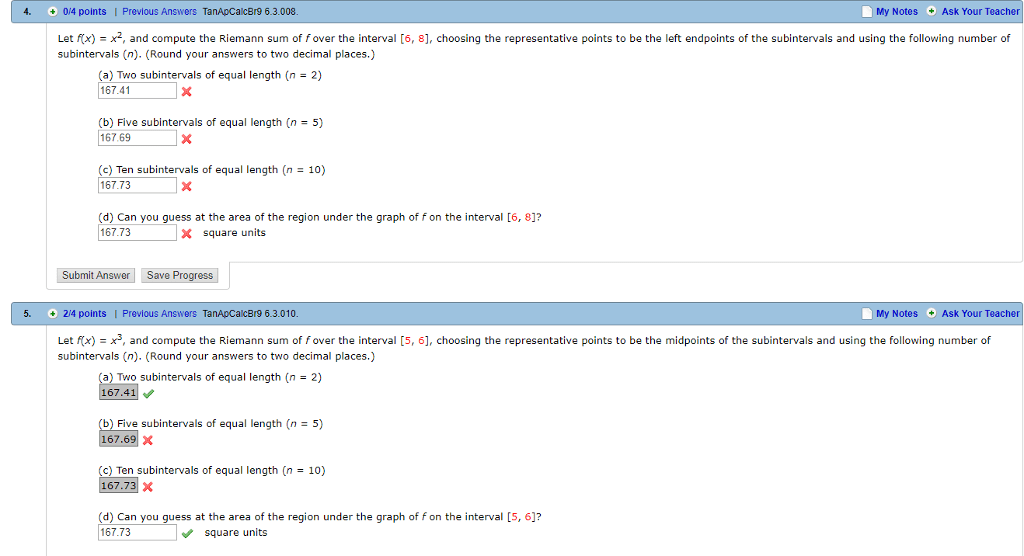
Consider the function f(x) = x on [0, 5]. What is the area a under the graph? x. If we divide the interval [0, 5] into n equal subintervals with length. A is the area of a triangle, so a =. The area between the function and x-axis in [xi 1, xi] can be approximated by thin rectangle if. Add all the thin rectangles together, we have. --- riemann sum is small enough, i. e n is big enough. If exists, we denote which is called . If f is continuous on the interval [a, b] and f is any antiderivative of f on [a, b], then. Example 8. 4: find the area of a region in the figure. y = x2. 0 3 b a kf dxx k b a dxxf k constant b a xf xg dx b a dxxf b a dxxg b a dxxf.