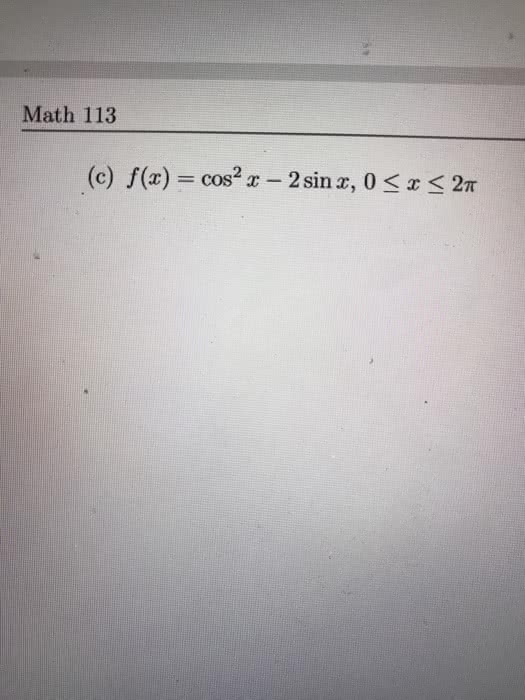MATA32H3 Lecture Notes - Lecture 15: Minimax, If And Only If, Nipple

• School: UTSC
• Department: Mathematics
• Course: MATA32H3
• Professor: Raymond Grinnell

Document Summary

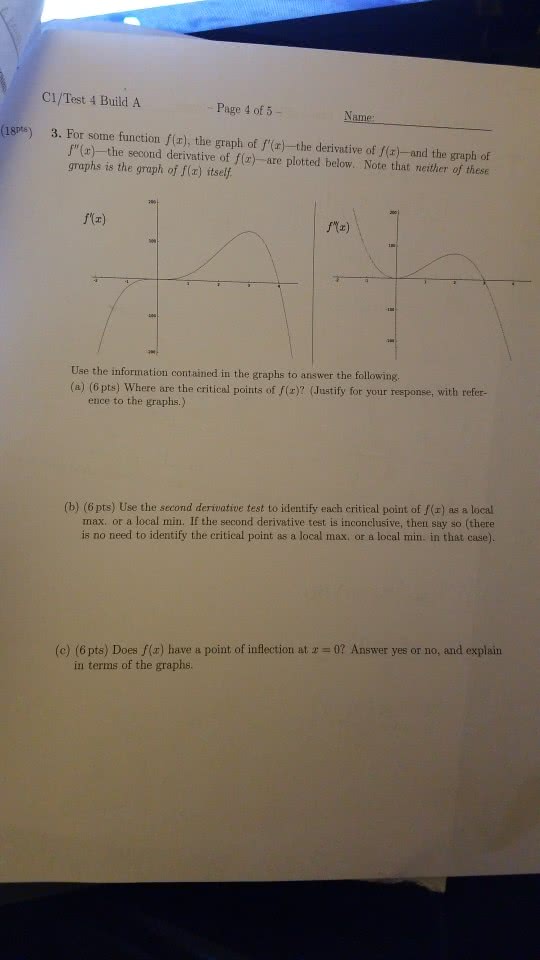
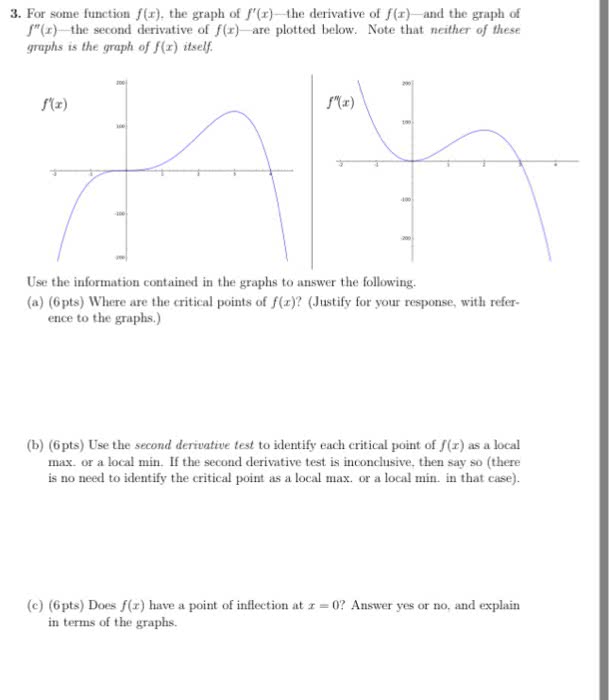
Idea: given y=f(x), the 1st derivative is used to determine whether a critical number of a function is a local max, min, or neither. Let y=f(x) be a function and assume c" is a critical number of y". Gives information about the bending upwards/downwards of a function (i. e. concavity (point of inflection) Suppose we have a function y=f(x) so the f""(x) is defined on a given open interval (a,b) I: if f""(x) > 0 for all x of i, the f(x) is concave up on i, if f""(x) <0 for all x of i, then f(x) is concave down on i. We obtain intervals i, as in the concavity test: find f""(x, solve f"(x)=0, see if f""(x) is ever undefined. Definition: we have/say (c,f( c)) is a point of infection of y=f(x) where concavity changes. Note: 1st and 2nd derivative can often give information about extrema (max/min)