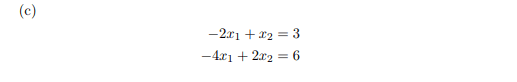MATA33H3 Lecture Notes - Lecture 6: Law And Justice, California State Route 2, 1

System of Linear Equations
Procedure for solving linear equations
Convert system into augmented matrix form 1.
Row Reduction: put. The augmented matrix into reduced matrix 2.
Convert back to equation form, read off the solution 3.
Ways to represent equations
Equation Form 1.
2. (Augmented) matrix form
3. Algebraic matrix form
Remark all 3 forms are equivalent in terms of solving the system of equations
What are they good for?
Simplicity of representation i.e. it tells you this is a system of linear equations 1.
Row Reduction 2.
Good to demonstrate algebraic properly of the coefficient matrix and allows solution to all RHS simultaneously 3.
if we can find , then we know to compute
Types of Solution
No solution 1.
i.e. if there is a solution then 0=1. Hence no solution exists
2. Unique solution
3. Infinitely many soultions
Summary: Given a system of linear equations and a reduced augmented matrix if
There is a row with all zeros to the left of the dividing line and a non-zero entry to the right, then the system has no solution 1.
Let n = # of unknowns, m = # of rows with leading 1 in the reduced matrix, if n = m then you have a unique solution, 2.
provided all other rows are identically zero
If m<n, and all other rows are zeros, then there are infinitely many solutions 3.

3
MATA33H3 Full Course Notes
Verified Note
3 documents
Document Summary
Convert back to equation form, read off the solution. 1: (augmented) matrix form, algebraic matrix form. Remark all 3 forms are equivalent in terms of solving the system of equations. Summary: given a system of linear equations and a reduced augmented matrix if. 2. i. e. if there is a solution then 0=1. Hence no solution exists if we can find , then we know to compute. Simplicity of representation i. e. it tells you this is a system of linear equations. Good to demonstrate algebraic properly of the coefficient matrix and allows solution to all rhs simultaneously. There is a row with all zeros to the left of the dividing line and a non-zero entry to the right, then the system has no solution. Let n = # of unknowns, m = # of rows with leading 1 in the reduced matrix, if n = m then you have a unique solution, provided all other rows are identically zero.