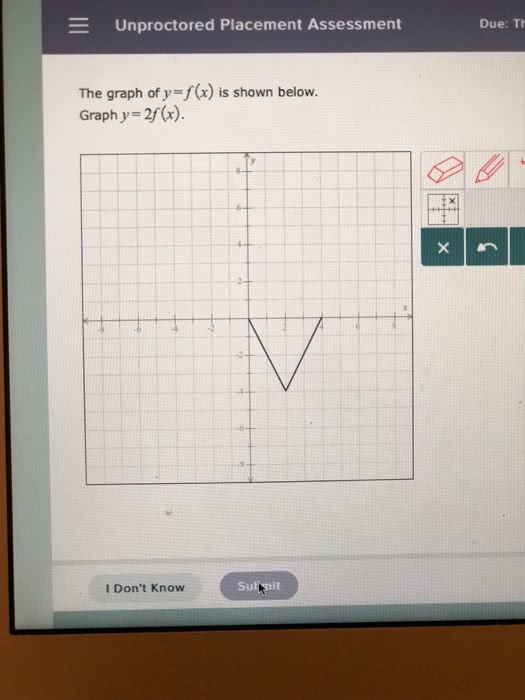
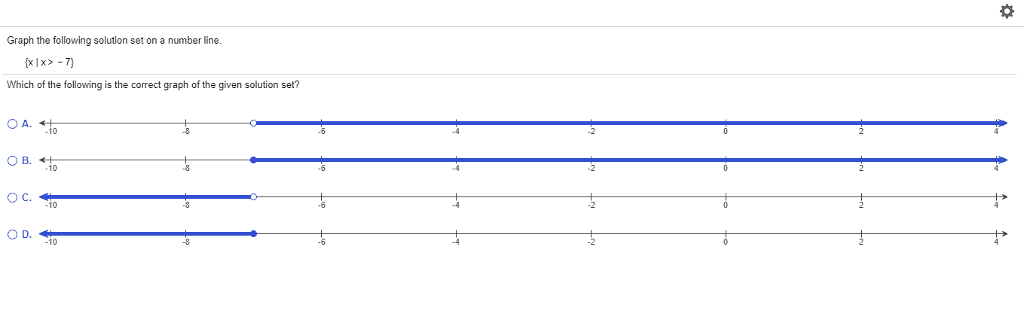
MATA67H3 Lecture 4: w4
Document Summary
Pascal was not the rst to discover the triangle of binomial coef- Cients but was given credit because of how he related it to his work with probability and expectation. The triangle may have rst appeared more than 300 years earlier during the 11th century in china: Rephrase the problem as an arrangement we already know. The number of ways to distribute r identical objects into n distinct boxes with at least one object in each box is c(n . We need to place n of the r objects amongst the n boxes leaving us with r n objects to distribute into the n boxes. Whenever we have restrictions on the number of items in a box, we can subtract those items from the total we are choosing from. The number of ways to distribute r identical objects into n distinct boxes with at least ri objects in the ith box is. Rn) + n 1, n 1)
th root of 2 as 
?
. What happens to the 
