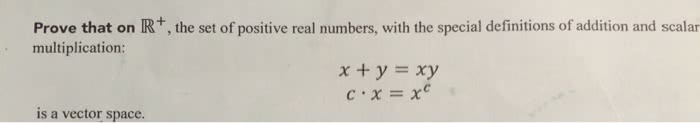MATB24H3 Lecture Notes - Unit Vector, Dot Product, Row And Column Spaces
Document Summary
In this section we will develop a process that will give us a basis of a subspace. W of rn with the property that any two vectors in this basis are orthogonal and unit vectors. Definition: let {v1, v2, vk} be a set of nonzero vectors in rn. We say that this set is orthogonal if vi vj = 0 for all i, j {1, 2, k} such that i 6= j. Theorem: let {v1, v2, vk} be an orthogonal set of vectors in rn then this set is independent. proof. 0 = r1v1 + r2v2 + + rkvk then vi 0 = vi (r1v1 + r2v2 + + rkvk) thus, 0 = r1(vi v1) + r2(vi v2) + + ri(vi vi) + + rk(vi vk) or 0 = ri||vi||2 since vi 6= 0 then ||vi|| 6= 0 therefore ri = 0.