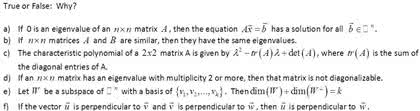MATA23H3 Lecture : Eigenvalues, eigenvectors, and diagonalization
Document Summary
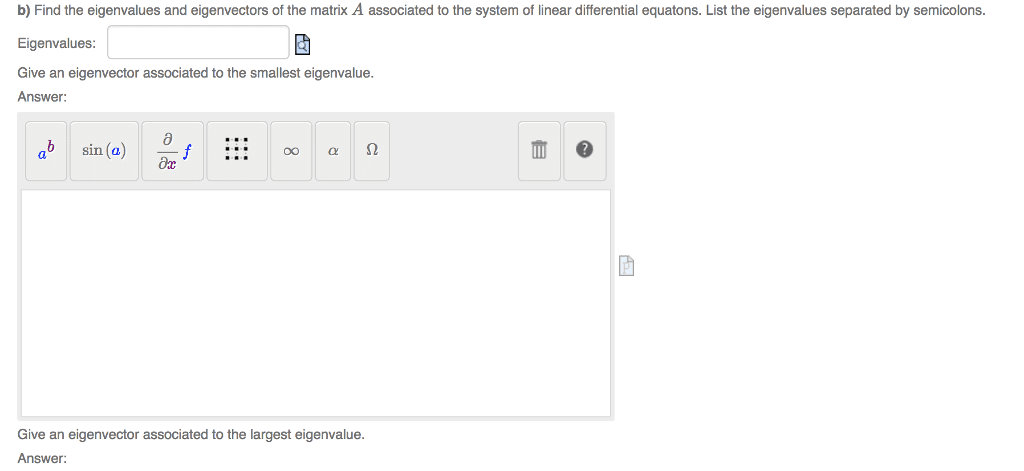
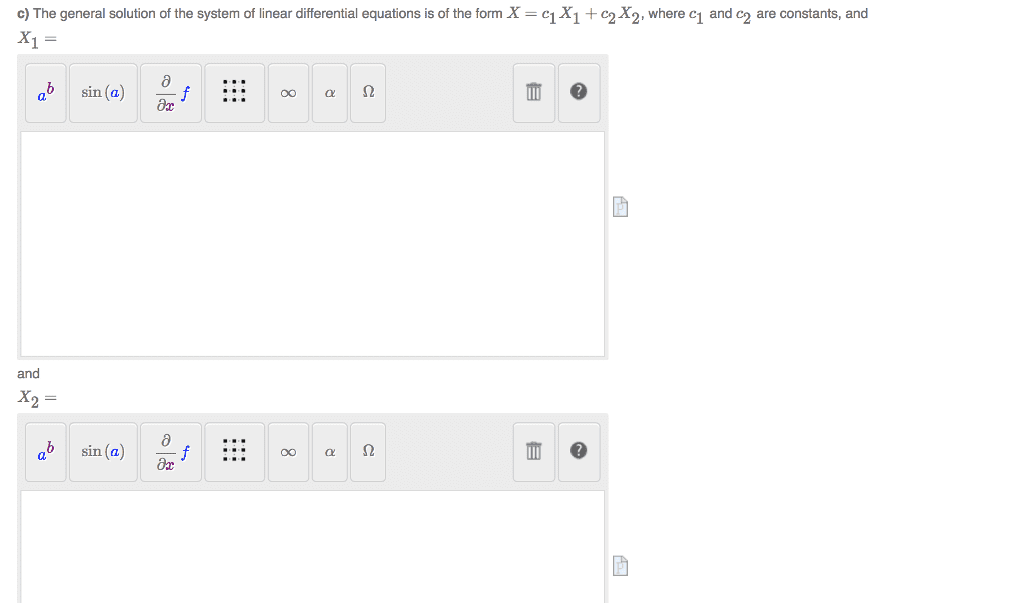
Let a be an n n matrix. A scalar is an eigenvalue of a if there is a. De nition: nonzero vector v rn, such that av = v. In this case, v is called an eigenvector of a corresponding to the eigenvalue . How to find the eigenvalues of a square matrix. De nition: let a be an n n matrix. The characteristic polynomial of a is given by p( ) = |a i|. If is an eigenvalue of a, then the set is called the eigenspace of . It contains the zero vector and all the eigenvectors of a corre- sponding to . Note: e = nullspace( a i ). www. notesolution. com. 1 3 2: find the characteristic polynomial of a, find all of the eigenvalues of a, for each eigenvalue of a, nd its eingespace e . www. notesolution. com.