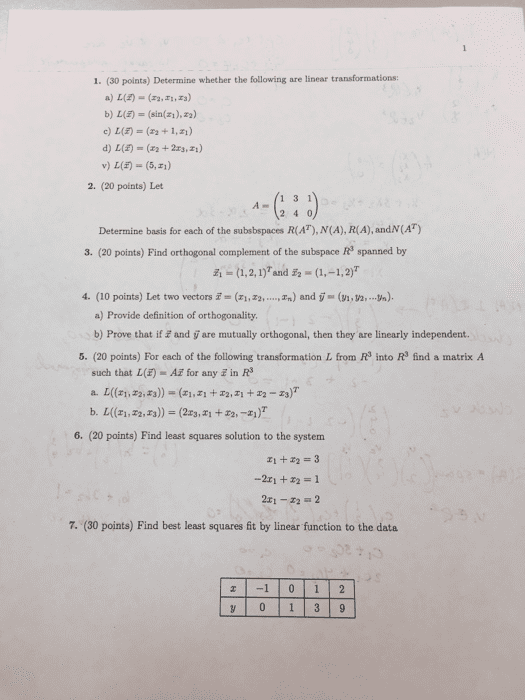MATB24H3 Lecture Notes - Symmetric Matrix, Parallelogram, Linear Map

188 views5 pages

greencod217

21 Apr 2013

School

Department

Course

Professor

For unlimited access to Class Notes, a Class+ subscription is required.

Document Summary

, an be n linearly independent vectors in. , then the volume of the n-box is: In case we have an m-box in rm, then its volume would be |det(a)|. Note: (1)a is an m n matrix. We cannot get the determinant of a matrix which is not a square matrix! (2) at a is a square matrix. (3) at a is a symmetric matrix. (4) if m = n, then: A 1-box in rm: the 1-box determined by the vector a1 is the line segment pdet(at a) = pdet(at )det(a) = pdet(a)det(a) = p(det(a))2 = |det(a)|. from the origin to the tip of a1. It"s volume is: pdet(at a) = vuuut(cid:2) a1 (cid:3) the length of a1. Thus the length of a 1-box is its length. a1. = a1 a1 = pka1k2 = ka1k, A 2-box in rm: it is a parallelogram with a vertex at the origin.

Related Questions

Test review

ey table is seen below xeecions tor Chapter 1 12, Fori, b â¬ Î.el * b-aa (0 (D 14 ForVEQ r the operation defined in Example 1 on the wr John Sue Henry. P iDFor 15ine if is ass ociative by determining if the final six engu defined ang property (ii)of Theorem 1 . So no element i if the operntion debined in Example 1 of Emle if each element has an inverse Section 1.3 Groups iw comutatityn ild Chapter 3 where the Funda the exercises that follow etermining why they are not Write out the Cayley table for the gru(o)nud lensify thee element the 10 elements of the group Z 18 its operation uses ts in the first coordinnte and +2 in the secotu Ldessity the Zn and write out the Cayley table. Reeall th of each element does Theorem 1.14 tell us aont the entries in the Cayley table ol s xrewp that is set with exactly one element. A {n), will always form group since there 19. What nly one way to define an operation on the set. Be sure to shhow that the properi combination of the usual notice what set the rule is be of a group all hold. 21. We can create even create groupe with games! Consider four cups placed in a ssare patter table. If we have a penny in one of the cups there are four ways we can move it to t cup: Horizontally, Vertically, Diagonally, or Stay nehere it is. We will p, S. To define nn operation, consider two movements in a row, v.e.,m ove the penny as r tells us to, then after that move the penny as y instruets. the set of integers the set of real numbers n the set of positive integers. e set of positive integers. n the set of positive integers. on the set of integers e set of negative integers. we ple, HV D since if we first move it horizontally and then vertically nltogether e moved it diagonally. Create the Cayley table for this group, identify the identity and the inverse of cach element 22. Prove that the set A 0 under matrix multiplication. Is it abelian? 23. Verify that 3(R) is a group using the addition of funetions as defined in Example 13 e set of nonzero rational n he set of nonzero real num n on the set R (-1 Section 1.4 Basic Algebra in Groups 24. Prove the Cancellation Law (Theorem 1.20). Do not use any theorems that occur after it in the text ssociative, commutative, has roof or counterexample fo 25. Assume G is a group and a e G. Consider a fixed integer k and use PMI (Theorem 0.3) to prove that for all nEN, a aYou will need to consider cases here since k can be positive, negative, or o 26. Prove Theorem 1.23 (ii) for the case of n > 0 and m

I need help on number 2. I can't seem to find alocal max or min let alone the absolute.

Overview: You will identify, solve, and fully analyzea "real world" optimization problem of your choosing. It should bea problem that we did not cover in class, but you are free toconsult other sources for inspiration. If you get your idea fromanother source, you should both cite it and add some originalthoughts to your write-up.

Details: What you hand in to me should consist of thefollowing parts:

(1) An introduction clearly stating theproblem to be solved, including any necessary explanation of theset-up as well as clearly defined variables, parameters, etc. Theportion should be written out in full sentences. In particular, youshould identify the quantity to optimized (i.e., maximized orminimized) and identify any constraints or boundary conditions. Thequantity being optimized should be a function of two or morevariables.

WHAT I NEED HELP ON----->(2) A translationof the story problem in part (1) to a purely mathematical problem.You should then fully solve the mathematical problem by (i) findingand classifying all critical points, (ii) analyzing the boundariesor constraints, and (iii) deciding the absolute max/min value andwhere it occurs.

(3) A brief conclusion in which you discussthe implications of the mathematics in part (2) for the originalstory problem. This portion should also be written in fullsentences.

---so far what I have done--

The pool is an open top consisting of a rectangle and a semicircle. I put a constraint on volume and set it equal to10000 m^3 . So What I am trying to figure out is whatdimensions create the lowest surface area. I found a local minat r= 7.815,w=15.631 but that means that their would be noheight for the box. does that make sense? are theirother points I should be checking?

so far I have

V=2rwh+.5pi(r^2)w

h=(V-.5pi(r^2)w)/2rw

S=4rh+2wh+pi(r)w+pi(r^2)

S=2V/w+V/r+.5w(pi)r

partials are

Sr=-V/r^2 +.5w(pi)

Sw=-2V/w^2+.5pi(r)

Srr=2V/r^3

Sww=4V/w^3

Swr=.5(pi)

MATB24H3 Lecture Notes - Symmetric Matrix, Parallelogram, Linear Map

Document Summary

Get access

Related Documents

MATB24H3 Lecture Notes - Orthogonal Matrix, Symmetric Matrix, Row And Column Vectors

MATB24H3 Lecture Notes - Unit Vector, Dot Product, Row And Column Spaces

MATB24H3 Lecture Notes - Linear Map, Row And Column Spaces, Symplectic Group

Related Questions