MAT136H1 Lecture Notes - Quadratic Equation, Asymptote

• School: UTSG
• Department: Mathematics
• Course: MAT136H1
• Professor: all

Document Summary

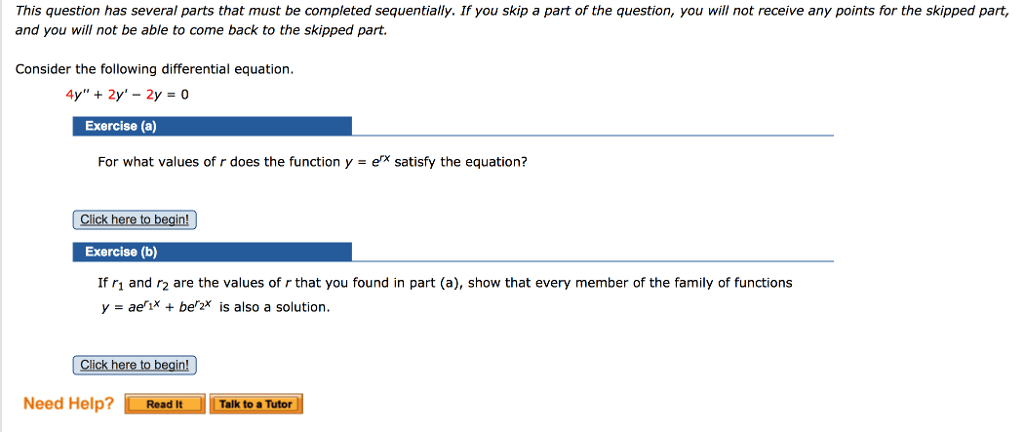
Question #2 (medium): forming functions to satisfy differential equation. Given the differential equation, take the first and second derivative if necessary then equate to the differential equation to get missing parameters. Then with those determined values, plug into the family of the function given, simplify and show that it equals to the other side. Sample question: for what values of does the function satisfy the differential equation, if and are values of found in part 1) show that every member of the family of function is also a solution. Move all to one side: , since for any value of 0 because it is its horizontal asymptote, it can be dropped, so: . Then it looks like a quadratic equation which can be factored: ( )( ) . Thus: and denote the two solutions found in part 1) so form.