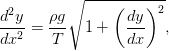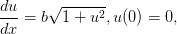MAT136H1 Lecture Notes - Product Rule, Integrating Factor

27 views1 pages

ultramarineeel914

8 Apr 2013

School

Department

Course

Professor

For unlimited access to Class Notes, a Class+ subscription is required.

plummouse698 and 39596 others unlocked

MAT136H1 Full Course Notes

Verified Note

92 documents

Document Summary

Question #4 (medium): solving the initial value for the linear differential equation. Solving initial value means once the linear differential equation has been solved, given the x and y value combination, the arbitrary constant factor can be determined by working out the equation backward. First the equation need to be arranged in the form of linear differential equation: The integrating factor is: ( ) . Multiply the integrating factor to the linear differential equation on both sides: ; the left side is then in the form of product rule: ( The equation can be divided by the integrating factor: Now since ( ) , plug into the equation and to find the missing value :

Related Questions

must understand functions to be able linearize. First let's review what graphs of certain functions looks like. Sketch the shape of each type of y vs. x function below. k is listed as a generic constant of proportionally. Linear y = kx Inverse y = k/x Inverse Square y = k/x^2 Power y = kx^2 You will notice that only the linear function is a straight line. We can easily find the slope of our line by measuring the rise and dividing it by the run of the graph or calculating it using two points. The value of the slope should equal the constant, k, from the equation. Finding k is a bit more challenging in the last three graphs because the slope isn't constant. This should make sense since your graphs aren't linear. So how do you calculate the constant, k? You need to transform the non-linear graph into a linear graph in order to calculate a constant slope. You can accomplish this by transforming one or both of the axes for the graph. The hardest part is figuring out which axes to change and how to change them. The easiest way to accomplish this task is to solve your equation for the constant. Note in the examples from the last page there is only one constant, but this process could be done for other equations with multiple constants. Instead of solving for a single constant, put all of the constants on one side of the equation. When you solve for the constant, the other side of the equation should be in fraction form. This fraction gives the rise and run of the linear graph. Whatever is in the numerator is the vertical axis and the denominator is the horizontal axis. If the equation is not in fraction form, you will need to inverse one or more of the variables to make a fraction. First let's solve each equation to figure out what we should graph. Then look below at the example and complete the last one, a sample AP question, on your own. State what should be graphed in order to produce a linear graph to solve for k. Inverse Graph Vertical Axis: _____ Horizontal Axis: _____ Inverse Square Graph Vertical Axis: _____ Horizontal Axis: _____ Power (Square) Graph Vertical Axis: _____ Horizontal Axis: _____

Using a technique of integration and the separation-of-variables technique, you'll discover a function whose antiderivative models the shape of an ideal cable suspended from its endpoints. The function depends on a parameter b, which is determined by the properties of the cable, such as the density of the material out of which it is made.

Using principles from physics, it can be shown that when a perfectly flexible, uniformly dense, and inextensible cable is suspended from its endpoints, then it will assume a shape of a curve y = f(x) satisfying the following second-order differential equation:

where Ï is the density of the material of the cable, g is the acceleration due to gravity, and T is the magnitude of the tension in the cable at its lowest point.

We assume our cable is as in the diagram above and y = f(x) is its shape function; thus, not only does y satisfy the "hanging cable differential equation" above, we also have y '(0) = 0. Hence, making the substitution u =dy/dx in our the hanging cable equation, we obtain the first order, initial-value problem satisfied by u:

where b = Ïg/T Solve the preceding initial-value problem, entering your (explicit) solution in the form u = g(x) where g is a function of x in which the constant b is present.

MAT136H1 Lecture Notes - Product Rule, Integrating Factor

MAT136H1 Full Course Notes

Document Summary

Get access

Related Documents

MAT136H1 Lecture Notes - Product Rule, Linear Differential Equation, Integrating Factor

MAT136H1 Lecture Notes - Product Rule, Linear Differential Equation, Integrating Factor

MAT136H1 Lecture Notes - Product Rule, Integrating Factor

Related Questions