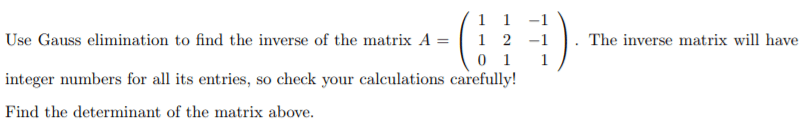MAT224H1 Lecture : Fields, Vector Spaces and Vector Subspaces
Document Summary
To do linear algebra we only need to do arithmetic operations to numbers. So instead of numbers we can work with anything we can add, multiply, subtract and divide (with the usual properties of the operations being assumed). Example: the inverse of a matrix (cid:16)1 2. 2 (cid:17) because nding inverse matrix involves only arithmetic operations, the entries of the matrix we started with are rational and thus the answer should be a matrix with rational entries only. The relevant de nition here is that of a eld: A set k with operation + and is called a eld if: Sum of two numbers is a number x + y k for all x, y k. Order doesn"t matter for addition x + y = y + x for all x, y k. Grouping doesn"t matter for addition (x+y)+z=x+(y+z) for all x, y, z k.