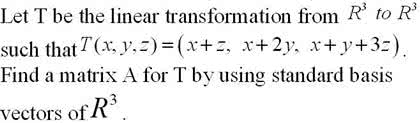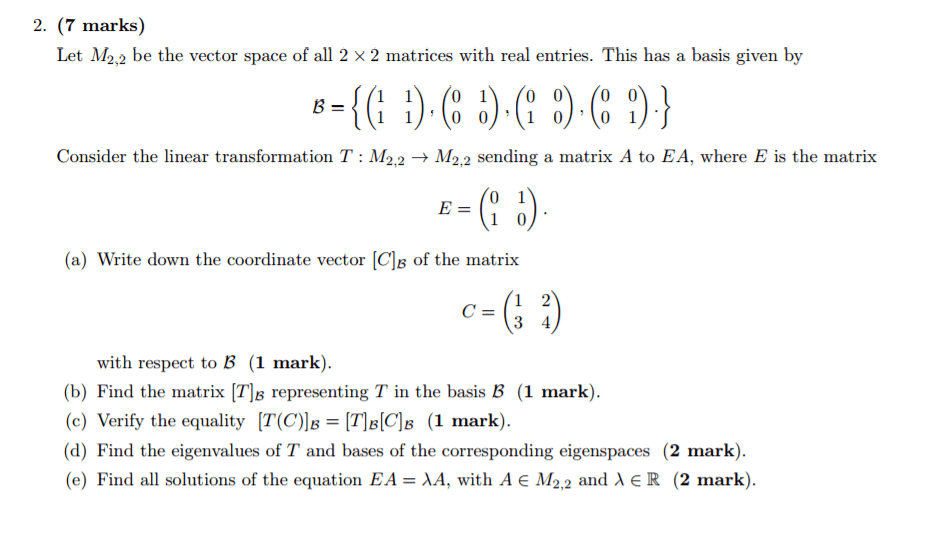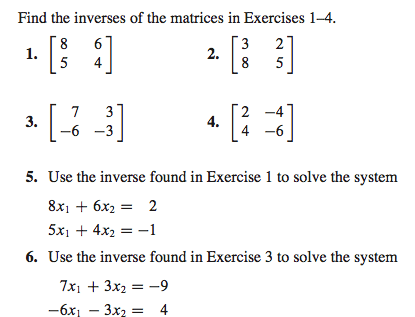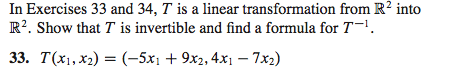Please show all work for credit and I only need questions number6, 27C, 28, and 33
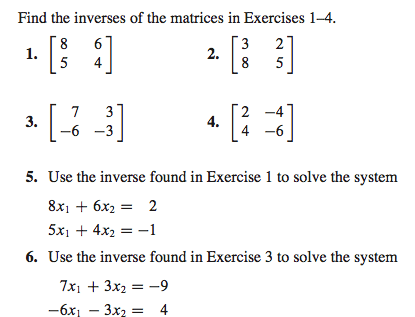


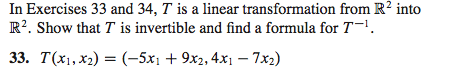
Find the inverses of the matrices in Exercises 1-4. Use the inverse found in Exercise 1 to solve the system Use the inverse found in Exercise 3 to solve the system Let A be a 3 times 3 matrix. Use equation (2) from Section 2.1 to show that row, (A) = row, (I) -A, for i = 1,2,3. Show that if rows 1 and 2 of A are interchanged, then the result may be written as EA, where E is an elementary matrix formed by interchanging rows 1 and 2 of I. Show that if row 3 of A is multiplied by 5, then the result may be written as EA, where E is formed by multiplying row 3 of I by 5. Let A and B be n times n matrices. Show that if AB is invertible, so is B. In Exercises 33 and 34, T is a linear transformation from R2 into R2. Show that T is invertible and find a formula for T-1