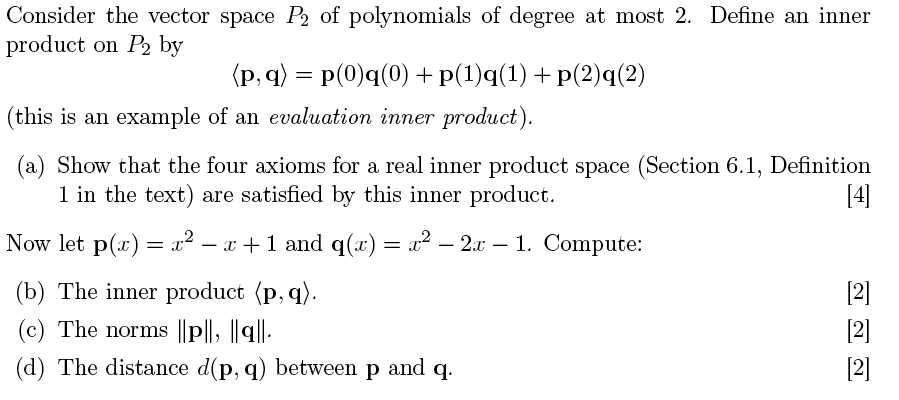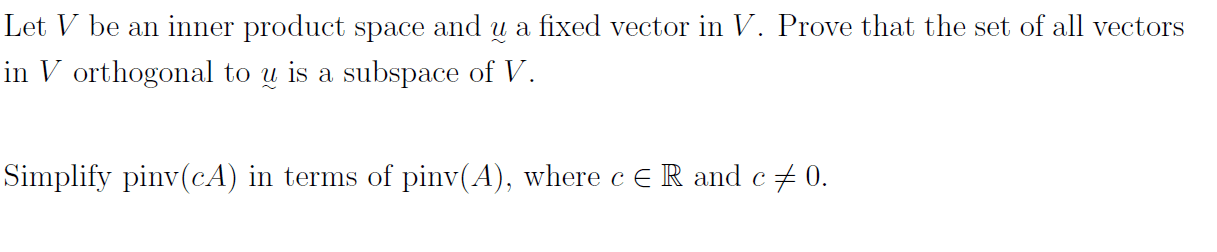MAT224H1 Lecture : dot product, inner product spaces and coordinates, orthogonal bases, hermitian matrices
Document Summary
1 reminder about dot product on rn xn(cid:19) and w = (cid:18)y1. Recall that on rn the dot product of vectors v = (cid:18)x1 yn(cid:19) is de ned by the equation v w = x1y1 + . Linearity: (c1v1 + c2v2) w = c1v1 w + c2v2 w. Symmetry: v w = w v. Positivity: v v > 0 for v 6= 0. The dot product on rn is good for doing geometry in n-dimensional space: measuring lengths, angles, areas and so on. But this is more or less all it is good for. However there are similar notions on other vector spaces, e. g. spaces of functions in analysis or random variables in statistics. These notions allow us to answer questions how close are two functions to each other , how correlated are two events and so on. We will now de ne what an inner product is as a generalization of the notion of the dot-product on.