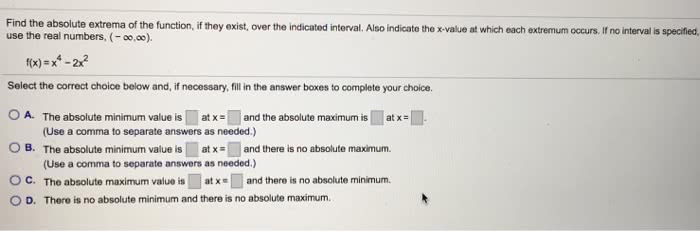
Help with 4,6,12,17,30 please
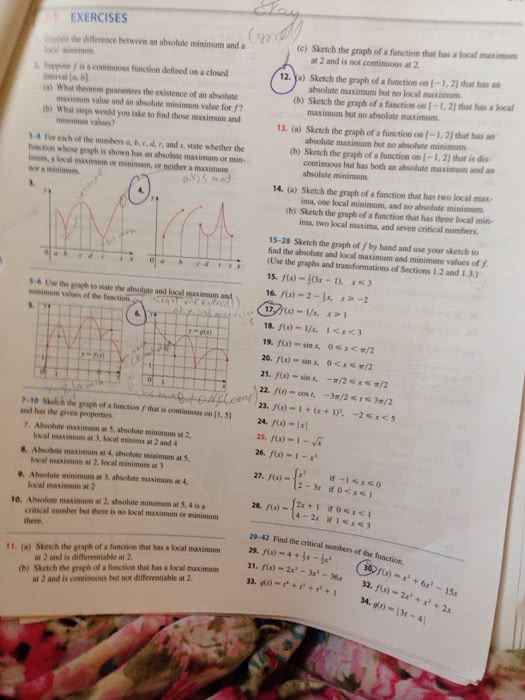
EXERCISES lin the difference between an absolute minimum and a (c) Sketch the graph of a function that has a local maxmm at 2 and is not continuous at 2 Saypose fis a continuoes function defined on a closed 12. Ya) Sketch the graph of a function on 1-1,21 that has an val [a,b). maxinwm value and an absolute minimem value for f minimun vales? absolute maximum but no local maximum (b) Sketch the graph of a function on [-1,21 that has a loca ia) What theorem guarantees the existence of an absolute b) What steps would you take to find those maximum and 34 For esxch of the numbers a, b,c,d, r, and s, state whether the maximum but no absolute maximum. 13. (a) Sketch the graph of a function on -1,21 that has an absolute maximum but no absolute minimum (b) Sketch the graph of a function on [-1,21 that is dis funscticon whoue gragh is shown has an ahsolate maximum or min akval maximem or minimum, or neither a maximum continuous but has both an absolute maximum and an absolute minimum imim, 14. (a) Sketch the graph of a function that has two local max- ima, one local minimum, and no absolute minimum (b) Sketch the graph of a function that has three local min- ima, two local maxima, and seven critical numbers. 15-28 Sketch the graph of f by hand and use your sketch to (Use the graphs and transformations of Sections 1.2 and 1.3.) 15, f(x)-jar-1),ã3 find the absolute and local maximum and minimum values of f De s-6 Use te gragh to state the absolute and local maximam einimum vaues of the function 2o.fu) _ san x. 0